Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) (H) có các đường tiệm cận là:
- Tiệm cận ngang y = -1
- Tiệm cận đứng x = -1
hai đường tiềm cận này cắt nhau tại điểm I(-1; -1).
Hình (H') có hai đường tiệm cận cắt nhau tại I'(2;2) nên ta cần phép tịnh tiến theo vector \(\overrightarrow{II'}=\left(2-\left(-1\right);2-\left(-1\right)\right)=\left(3;3\right)\)
b) Hình (H') có phương trình là:
\(y+3=\dfrac{3-\left(x+3\right)}{\left(x+3\right)+1}\) hay là \(y=\dfrac{-4x-12}{x+4}\)
Hình đối xứng với (H') qua gốc tọa độ có phương trình là:
\(-y=\dfrac{-4\left(-x\right)-12}{-x+4}\) hay là: \(y=\dfrac{4x-12}{-x+4}\)

Từ đồ thị hàm số (H), để có hình (H’) nhận y = 2 là tiệm cận ngang và x = 2 là tiệm cận đứng, ta tịnh tiến đồ thị (H) song song với trục Oy lên trên 3 đơn vị, sau đó tịnh tiến song song với trục Ox về bên phải 3 đơn vị, ta được các hàm số tương ứng sau:
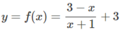
![]()
![]()

1.
\(\lim\limits_{x\rightarrow\infty}\frac{3x-2}{x+1}=3\Rightarrow y=3\) là tiệm cận ngang
2.
\(\lim\limits_{x\rightarrow2}\frac{-2x}{x-2}=\infty\Rightarrow x=2\) là tiệm cận đứng
3.
\(\lim\limits_{x\rightarrow\infty}\frac{x-2}{x^2-1}=0\Rightarrow y=0\) là tiệm cận ngang
4.
\(\lim\limits_{x\rightarrow\infty}\frac{x-1}{x^2-x}=0\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow0}\frac{x-1}{x^2-x}=\infty\Rightarrow x=0\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow1}\frac{x-1}{x^2-x}=1\) hữu hạn nên \(x=1\) ko phải tiệm cận đứng
ĐTHS có 2 tiệm cận

1, Đổi chỗ 3 viên ở 3 đỉnh tam giác: viên dưới cùng lên đỉnh trên cùng, 2 viên ngoài cùng ở 2 bên đảo xuốn đáy
2, 8-6+2=4; 12-5+8=15; 13-10+15=18. x=15
3,
*) \(5^3+5=130;3^3+3=30;2^3+2=10;1^3+1=2\)
*) 2+3=8 hay 2.(2+3)-2=8
4+5=32 hay 4.(4+5)-4=32
5+8=60 hay 5.(5+8)-5=60
6+7=72 hay 6.(6+7)-6=72
7+8= 7.(7+8)-7=98

b) Tiệm cận đứng là đường thẳng \(x=3\)
Tiệm cận ngang là đường thẳng \(y=1\)


ĐKXĐ: \(0< x\le2\)
Miền xác định của hàm không chứa vô cùng nên hàm ko có tiệm cận ngang
\(\lim\limits_{x\rightarrow0^+}\frac{\sqrt{2-x}}{\left(x-1\right)\sqrt{x}}=-\infty\) nên \(x=0\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow1}\frac{\sqrt{2-x}}{\left(x-1\right)\sqrt{x}}=\infty\) nên \(x=1\) là tiệm cận đứng
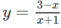 có đồ thị (H)
có đồ thị (H)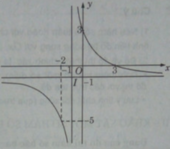
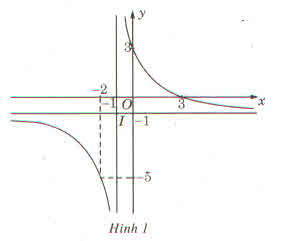

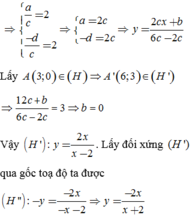





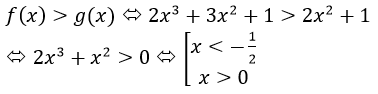
a) Từ đồ thị hàm số (H), để có hình (H’) nhận y = 2 là tiệm cận ngang và x = 2 là tiệm cận đứng, ta tịnh tiến đồ thị (H) song song với trục Oy lên trên 3 đơn vị, sau đó tịnh tiến song song với trục Ox về bên phải 3 đơn vị, ta được các hàm số tương ứng sau:
b) Lấy đối xứng hình (H’) qua gốc O, ta được hình (H’’) có phương trình là: