Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}-\frac{b}{2a}=-2\\\frac{4ac-b^2}{4a}=5\\a+b+c=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=4a\\4ac-b^2=20a\\c=1-a-b\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=4a\\4ac-b^2=20a\\c=1-5a\end{matrix}\right.\)
\(\Rightarrow4a\left(1-5a\right)-16a^2=20a\)
\(\Leftrightarrow-36a=16\Rightarrow a=-\frac{4}{9}\) \(\Rightarrow b=-\frac{16}{9};c=\frac{29}{9}\)
\(\Rightarrow S=\) bấm máy

\(y=ax^2+bx+c\left(d\right)\)
Do y có gtln là 5 khi x=-2
\(\Rightarrow\left\{{}\begin{matrix}5=a\left(-2\right)^2+b\left(-2\right)+c\\-\dfrac{b}{2a}=-2\\a< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}4a-2b+c=5\\4a-b=0\end{matrix}\right.\)
Có \(M\in\left(d\right)\Rightarrow a+b+c=-1\)
Có hệ \(\left\{{}\begin{matrix}4a-2b+c=5\\4a+b=0\\a+b+c=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-2}{3}\\b=-\dfrac{8}{3}\\c=\dfrac{7}{3}\end{matrix}\right.\)(tm)
Vậy...

a.
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=-2\\4a-2b+c=4\\c=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=4a\\4a-2.4a+6=4\\c=6\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=4a=2\\a=\dfrac{1}{2}\\c=6\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x^2+2x+6\)
b.
\(y_{min}=y_{CT}=\dfrac{4ac-b^2}{4a}=\dfrac{4.1.1-\left(-4\right)^2}{4.1}=-3\)
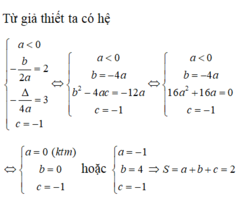
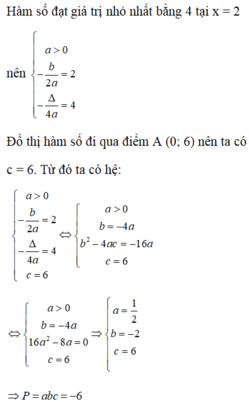
a/ Ta có hệ điều kiện:
\(\left\{{}\begin{matrix}-\frac{b}{2a}=2\\\frac{4ac-b^2}{4a}=4\\c=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=-4a\\24a-b^2=16a\\c=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-4a\\8a-16a^2=0\\c=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\frac{1}{2}\\b=-2\\c=6\end{matrix}\right.\) \(\Rightarrow P\)
b/ \(\left\{{}\begin{matrix}-\frac{b}{2a}=2\\\frac{4ac-b^2}{4a}=3\\c=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=-4a\\-4a-b^2=12a\\c=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-4a\\16a^2+16a=0\\c=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=4\\c=-1\end{matrix}\right.\) \(\Rightarrow S\)