NH
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 6 2023
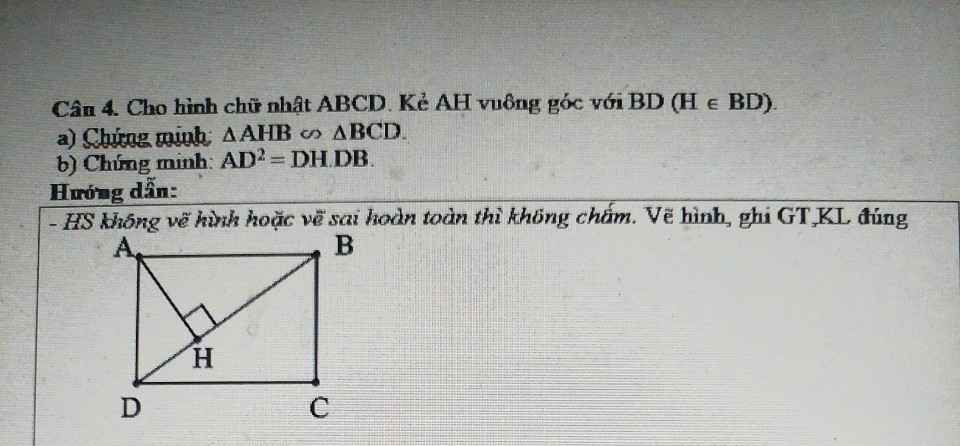
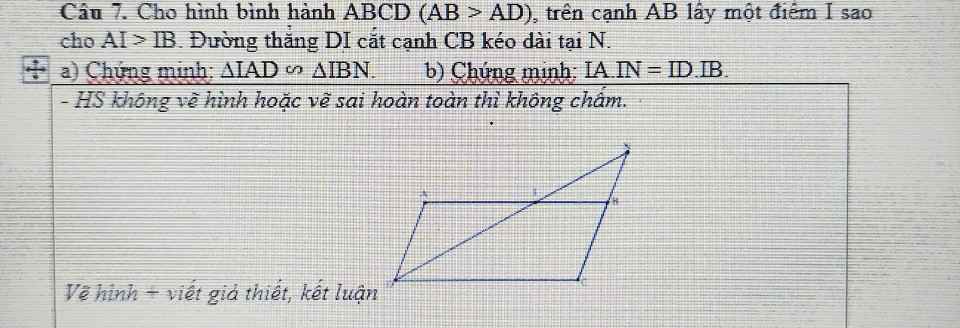
a: Xét ΔIAD và ΔIBN có
góc IAD=góc IBN
góc AID=góc BIN
=>ΔIAD đồng dạng với ΔIBN
b: ΔIAD đồng dạng với ΔIBN
=>IA/IB=ID/IN
=>IA*IN=IB*ID
16 tháng 6 2023
Xét ΔIAD và ΔIBN có
góc IAD=góc IBN
góc AID=góc BIN
=>ΔIAD đồng dạng với ΔIBN
=>IA/IB=ID/IN
=>IA*IN=IB*ID
m.người ơi
13 tháng 9 2023
BA=BC
=>góc BAC=góc BCA
=>góc BCA=góc DAC
=>AD//BC
=>ABCD là hình thang
27 tháng 1 2022
\(\frac{1-3x}{1+3x}-\frac{1+3x}{1-3x}=\frac{12}{1-9x^2}\left(ĐKXĐ:x\ne\pm\frac{1}{3}\right)\)
<=> \(\frac{\left(1-3x\right)^2}{\left(1+3x\right)\left(1-3x\right)}-\frac{\left(1+3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}=\frac{12}{\left(1-3x\right)\left(1+3x\right)}\)
=> \(\left(1-3x\right)^2-\left(1+3x\right)^2=12\)
<=> \(\left(1-3x-1-3x\right)\left(1-3x+1+3x\right)=12\)
<=> \(-12x=12\)
<=> \(x=-1\left(TMĐK\right)\)
Vậy: ...
TT
27 tháng 1 2022
\(\frac{12}{1-9x^2}=\frac{1-3x}{1+3x}-\frac{1+3x}{1-3x}\)
\(\Leftrightarrow\)\(\frac{12}{\left(1-3x\right)\left(1+3x\right)}=\frac{\left(1-3x\right)^2-\left(1+3x\right)^2}{\left(1-3x\right)\left(1+3x\right)}\)
\(\Rightarrow\)\(12=\left(1-3x\right)^2-\left(1+3x\right)^2\)
\(\Leftrightarrow\)\(12=\left(1-3x-1-3x\right)\left(1-3x+1+3x\right)\)
\(\Leftrightarrow\)\(12=\left(-6x\right).2\)
\(\Leftrightarrow\)\(12=-12x\)
\(\Leftrightarrow\)\(x=-1\)
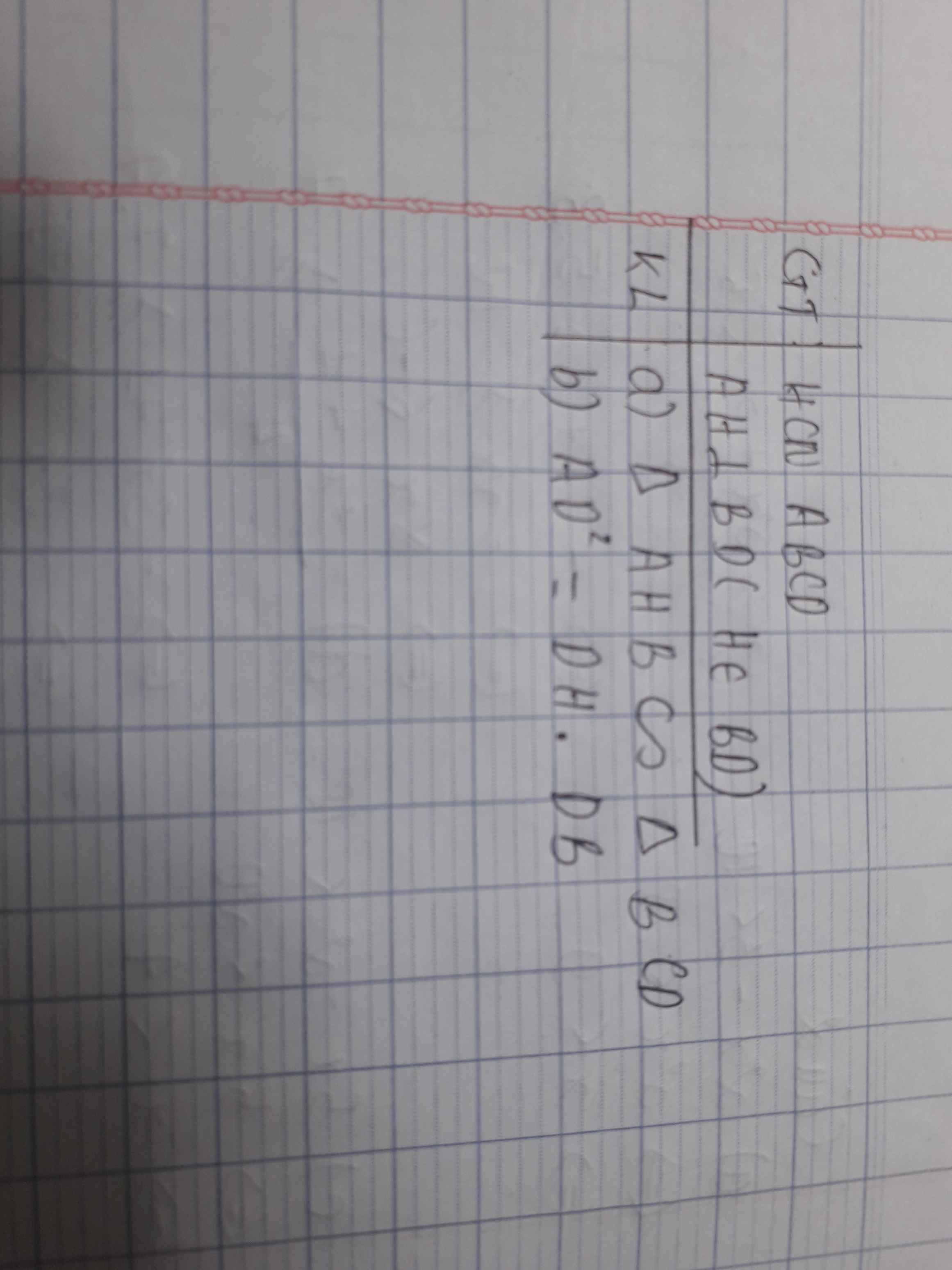
bằng 71122033447028553276 nha