K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
0
HN
0
22 tháng 3 2020
\(7a=9b=21c\Rightarrow\frac{7a}{63}=\frac{9b}{63}=\frac{21c}{63}\Leftrightarrow\frac{a}{9}=\frac{b}{7}=\frac{c}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{a}{9}=\frac{b}{7}=\frac{c}{3}=\frac{a-b+c}{9-7+3}=\frac{-15}{5}=-3\)
\(\Leftrightarrow\frac{a}{9}=-3\Rightarrow a=-27\)
\(\frac{b}{7}=-3\Rightarrow b=-21\)
\(\frac{c}{3}=-3\Rightarrow c=-9\)
\(\Rightarrow a+b+c=-27-21-9=-57\)
DM
2
20 tháng 9 2023
19/57 . 2 4/7 - 19/57 . 1 5/7 - 19/57
= 19/57 x ( 2 4/7 - 1 5/7 )
= 19/57 x 6/7
= 2/7
20 tháng 9 2023
\(\dfrac{19}{57}.2\dfrac{4}{7}-\dfrac{19}{57}.1\dfrac{5}{7}-\dfrac{19}{57}\)
\(\text{=}\dfrac{19}{57}.\left(2\dfrac{4}{7}-1\dfrac{5}{7}-1\right)\)
\(\text{=}\dfrac{19}{57}.\left(\dfrac{-1}{7}\right)\)
\(\text{=}\dfrac{-1}{21}\)
NM
5
PT
1
CM
23 tháng 3 2019
12 , 5. − 5 7 + 1 , 5. − 5 7 = − 5 7 . 12 , 5 + 1 , 5 = − 5 7 .14 = − 10
23 tháng 7 2017
1/7=0,14289(57)
0,1428(57)<0,4128(57)
1/7<0,4128(57)
k và kb nhé
PT
1
CM
19 tháng 5 2019
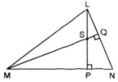
Trong ΔMNL có:
LP ⊥ MN nên LP là đường cao của ΔMNL.
MQ ⊥ NL nên MQ là đường cao của ΔMNL.
Mà LP, MQ cắt nhau tại điểm S
Nên: theo tính chất ba đường cao của một tam giác, S là trực tâm của tam giác.
⇒ đường thẳng SN là đường cao của ΔMNL.
hay SN ⊥ ML.
TM
1
9 tháng 11 2015
0,(57)=0,(01).57 = \(\frac{1}{99}.57=\frac{19}{33}\)
0,(42)=0,(01).42=\(\frac{1}{99}.42=\frac{14}{33}\)
=>0,(57)+0,(42)=\(\frac{19}{33}+\frac{14}{33}=\frac{33}{33}=1\)
Vậy 0,(57)+0,)42)=1
= 7.58885276491228E7
75775584+6437788:57
= 75775584+112943.6491
=75888527.65