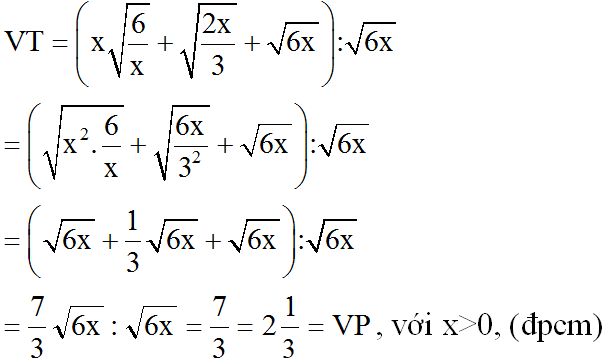K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
I
28 tháng 3 2020
đây là đề thi học sinh giỏi Bình định năm 2014-2015 ( mình đc cô giáo cho làm r nên bạn cứ yên tâm là đúng nhá . làm tỷ đề mà zẫn nhớ )
ta có \(x^3=\left(2+\sqrt{3}\right)-\left(2-\sqrt{3}\right)-3\sqrt[3]{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}.x\Rightarrow x^3+3x=2\sqrt{3}\left(1\right)\)
\(y^3=\left(\sqrt{5}+2\right)-\left(\sqrt{5}-2\right)-3\sqrt[3]{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}.y\Rightarrow y^3+3y=4\left(2\right)\)
Trừ theo zế của (1) cho (2) ta được
\(\left(x^3-y^3\right)+3\left(x-y\right)=2\sqrt{3}-4\)
do đó
\(A=\left(x-y\right)^3+3\left(x-y\right)\left(xy+1\right)=x^3-y^3-3\left(x-y\right)xy+3\left(x-y\right)xy+3\left(x-y\right)\)
\(=x^3-y^3+3\left(x-y\right)=2\sqrt{3}-4\)
CM
9 tháng 6 2018
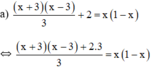
⇔ (x + 3)(x – 3) + 2.3 = 3x(1 – x)
⇔ x 2 − 9 + 6 = 3 x − 3 x 2 ⇔ x 2 − 9 + 6 − 3 x + 3 x 2 = 0 ⇔ 4 x 2 − 3 x − 3 = 0
Có a = 4; b = -3; c = -3 ⇒ Δ = ( - 3 ) 2 – 4 . 4 . ( - 3 ) = 57 > 0
Phương trình có hai nghiệm
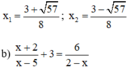
Điều kiện xác định: x ≠ 5; x ≠ 2.
Quy đồng và khử mẫu ta được :
(x + 2)(2 – x) + 3(2 – x)(x – 5) = 6(x – 5)
⇔ 4 − x 2 + 6 x − 3 x 2 − 30 + 15 x = 6 x − 30 ⇔ 4 − x 2 + 6 x − 3 x 2 − 30 + 15 x − 6 x + 30 = 0 ⇔ − 4 x 2 + 15 x + 4 = 0
Có a = -4; b = 15; c = 4 ⇒ Δ = 15 2 – 4 . ( - 4 ) . 4 = 289 > 0
Phương trình có hai nghiệm phân biệt:
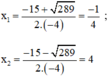
Cả hai giá trị đều thỏa mãn điều kiện.
Vậy phương trình có tập nghiệm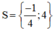 
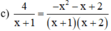
Điều kiện xác định: x ≠ -1; x ≠ -2.
Quy đồng và khử mẫu ta được:
4 ⋅ ( x + 2 ) = − x 2 − x + 2 ⇔ 4 x + 8 = − x 2 − x + 2 ⇔ 4 x + 8 + x 2 + x − 2 = 0 ⇔ x 2 + 5 x + 6 = 0
Có a = 1; b = 5; c = 6 ⇒ Δ = 5 2 – 4 . 1 . 6 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt:
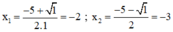
Chỉ có nghiệm x 2 = - 3 thỏa mãn điều kiện xác định.
Vậy phương trình có nghiệm x = -3.
PB
29 tháng 5 2021
a) a) Biến đổi vế trái thành 32√6+23√6−42√6326+236−426 và làm tiếp.
b) Biến đổi vế trái thành (√6x+13√6x+√6x):√6x(6x+136x+6x):6x và làm tiếp
HT
3
ML
9 tháng 8 2016
Bạn xem lại đề xem cố sai sót gì ko rồi comment vào "Trả lời" nhé.
13 tháng 1 2017
a)
\(\Leftrightarrow yz=z^2+2z+3\Leftrightarrow z\left(y-2-z\right)=3\)
\(\hept{\begin{cases}z=\left\{-3,-1,1,3\right\}\\y-2-z=\left\{-1,-3,3,1\right\}\end{cases}\Rightarrow\hept{\begin{cases}x=\left\{-2,0,2,4\right\}\\y=\left\{-2,-4,6,6\right\}\end{cases}}}\)
25 tháng 4 2021
LG a
12√48−2√75−√33√11+5√1131248−275−3311+5113;
Phương pháp giải:
+ Cách đổi hỗn số ra phân số: abc=a.c+bcabc=a.c+bc.
+ Sử dụng quy tắc đưa thừa số ra ngoài dấu căn:
√A2.B=A√BA2.B=AB, nếu A≥0, B≥0A≥0, B≥0.
√A2.B=−A√BA2.B=−AB, nếu A<0, B≥0A<0, B≥0.
+ √ab=√a√bab=ab, với a≥0, b>0a≥0, b>0.
+ √a.√b=√aba.b=ab, với a, b≥0a, b≥0.
+ A√B=A√BBAB=ABB, với B>0B>0.
Lời giải chi tiết:
Ta có:
12√48−2√75−√33√11+5√1131248−275−3311+5113
=12√16.3−2√25.3−√3.11√11+5√1.3+13=1216.3−225.3−3.1111+51.3+13
=12√42.3−2√52.3−√3.√11√11+5√43=1242.3−252.3−3.1111+543
=12.4√3−2.5√3−√3+5√4√3=12.43−2.53−3+543
=42√3−10√3−√3+5√4.√3√3.√3=423−103−3+54.33.3
=2√3−10√3−√3+52√33=23−103−3+5233
=2√3−10√3−√3+10√33=23−103−3+1033
=(2−10−1+103)√3=(2−10−1+103)3
=−173√3=−1733.
LG b
√150+√1,6.√60+4,5.√223−√6;150+1,6.60+4,5.223−6;
Phương pháp giải:
+ Cách đổi hỗn số ra phân số: abc=a.c+bcabc=a.c+bc.
+ Sử dụng quy tắc đưa thừa số ra ngoài dấu căn:
√A2.B=A√BA2.B=AB, nếu A≥0, B≥0A≥0, B≥0.
√A2.B=−A√BA2.B=−AB, nếu A<0, B≥0A<0, B≥0.
+ √ab=√a√bab=ab, với a≥0, b>0a≥0, b>0.
+ √a.√b=√aba.b=ab, với a, b≥0a, b≥0.
+ A√B=A√BBAB=ABB, với B>0B>0.
Lời giải chi tiết:
Ta có:
√150+√1,6.√60+4,5.√223−√6150+1,6.60+4,5.223−6
=√25.6+√1,6.60+4,5.√2.3+23−√6=25.6+1,6.60+4,5.2.3+23−6
=√52.6+√1,6.(6.10)+4,5√83−√6=52.6+1,6.(6.10)+4,583−6
=5√6+√(1,6.10).6+4,5√8√3−√6=56+(1,6.10).6+4,583−6
=5√6+√16.6+4,5√8.√33−√6=56+16.6+4,58.33−6
=5√6+√42.6+4,5√8.33−√6=56+42.6+4,58.33−6
=5√6+4√6+4,5.√4.2.33−√6=56+46+4,5.4.2.33−6
=5√6+4√6+4,5.√22.63−√6=56+46+4,5.22.63−6
=5√6+4√6+4,5.2√63−√6=56+46+4,5.263−6
=5√6+4√6+9√63−√6=56+46+963−6
=5√6+4√6+3√6−√6=56+46+36−6
=(5+4+3−1)√6=11√6.=(5+4+3−1)6=116.
Cách 2: Ta biến đổi từng hạng tử rồi thay vào biểu thức ban đầu:
+ √150=√25.6=5√6150=25.6=56
+ √1,6.60=√1,6.(10.6)=√(1,6.10).6=√16.61,6.60=1,6.(10.6)=(1,6.10).6=16.6
=4√6=46
+ 4,5.√223=4,5.√2.3+23=4,5.√83=4,5√8.334,5.223=4,5.2.3+23=4,5.83=4,58.33
=4,5.√4.2.33=4,5.2.√63=9.√63=3√6.=4,5.4.2.33=4,5.2.63=9.63=36.
Do đó:
√150+√1,6.√60+4,5.√223−√6150+1,6.60+4,5.223−6
=5√6+4√6+3√6−√6=56+46+36−6
=(5+4+3−1)√6=11√6=(5+4+3−1)6=116
LG c
(√28−2√3+√7)√7+√84;(28−23+7)7+84;
Phương pháp giải:
+ Cách đổi hỗn số ra phân số: abc=a.c+bcabc=a.c+bc.
+ Hằng đẳng thức số 1: (a+b)2=a2+2ab+b2(a+b)2=a2+2ab+b2.
+ Sử dụng quy tắc đưa thừa số ra ngoài dấu căn:
√A2.B=A√BA2.B=AB, nếu A≥0, B≥0A≥0, B≥0.
√A2.B=−A√BA2.B=−AB, nếu A<0, B≥0A<0, B≥0.
+ √ab=√a√bab=ab, với a≥0, b>0a≥0, b>0.
+ √a.√b=√aba.b=ab, với a, b≥0a, b≥0.
+ A√B=A√BBAB=ABB, với B>0B>0.
Lời giải chi tiết:
Ta có:
=(√28−2√3+√7)√7+√84=(28−23+7)7+84
=(√4.7−2√3+√7)√7+√4.21=(4.7−23+7)7+4.21
=(√22.7−2√3+√7)√7+√22.21=(22.7−23+7)7+22.21
=(2√7−2√3+√7)√7+2√21=(27−23+7)7+221
=2√7.√7−2√3.√7+√7.√7+2√21=27.7−23.7+7.7+221
=2.(√7)2−2√3.7+(√7)2+2√21=2.(7)2−23.7+(7)2+221
=2.7−2√21+7+2√21=2.7−221+7+221
=14−2√21+7+2√21=14−221+7+221
=14+7=21=14+7=21.
LG d
(√6+√5)2−√120.(6+5)2−120.
Phương pháp giải:
+ Cách đổi hỗn số ra phân số: abc=a.c+bcabc=a.c+bc.
+ Hằng đẳng thức số 1: (a+b)2=a2+2ab+b2(a+b)2=a2+2ab+b2.
+ Sử dụng quy tắc đưa thừa số ra ngoài dấu căn:
√A2.B=A√BA2.B=AB, nếu A≥0, B≥0A≥0, B≥0.
√A2.B=−A√BA2.B=−AB, nếu A<0, B≥0A<0, B≥0.
+ √a.√b=√aba.b=ab, với a, b≥0a, b≥0.
Lời giải chi tiết:
Ta có:
(√6+√5)2−√120(6+5)2−120
=(√6)2+2.√6.√5+(√5)2−√4.30=(6)2+2.6.5+(5)2−4.30
=6+2√6.5+5−2√30=6+26.5+5−230
=6+2√30+5−2√30=6+5=11.=6+230+5−230=6+5=11.
8 tháng 2 2021
1) Ta có: \(P=\left(\dfrac{\sqrt{x}}{2\sqrt{x}-2}+\dfrac{3-\sqrt{x}}{2x-2}\right):\left(\dfrac{\sqrt{x}-1}{x+\sqrt{x}+1}+\dfrac{\sqrt{x}+2}{x\sqrt{x}-1}\right)\)
\(=\left(\dfrac{\sqrt{x}}{2\left(\sqrt{x}-1\right)}+\dfrac{3-\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{3-\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{x-2\sqrt{x}+1+\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x+\sqrt{x}+3-\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{x-\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x+3}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x-\sqrt{x}+3}\)
\(=\dfrac{\left(x+3\right)\left(x+\sqrt{x}+1\right)}{2\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+3\right)}\)
KL
10 tháng 5 2021
B=\(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{6}{\sqrt{x}-1}-\dfrac{\sqrt{x}+15}{x+2\sqrt{x}-3}\) Bạn ơi giúp mk câu này vs ạ !
24 tháng 10 2015
ta có P(1)=1+a+b+c+d+e=3
P(2)=32+16a+8b+4c+2d+e=9
P(3)=243+81a+27b+9c+3d+e=19
P(4)=1024+256a+64b+16c+4d+e=33
P(5)=3125+625a+125b+25c+5d+e=51
<=> P(1)=a+b+c+d+e=2
P(2)=16a+8b+4c+2d+e=-23
P(3)=81a+27b+9c+3d+e=-224
P(4)=256a+64b+16c+4d+e=-991
P(5)=625a+125b+25c+5d+e=-3074
<=> 15a+7b+3c+d=-25
65a+19b+5c+d=-201
175a+37b+7c+d=-767
369a+61b+9c+d=-2083
<=> a=-15
b=85
c=-223
d=274
Nên e=-119
Vậy P(x)= x5-15x4+85x3-223x2+274x-119
=> P(6)=193
P(7)=819
P(8)=2649
P(9)=6883
P(10)=15321
P(11)=30483