K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 4 2023
`P(x)=\(4x^2+x^3-2x+3-x-x^3+3x-2x^2\)
`= (x^3-x^3)+(4x^2-2x^2)+(-2x-x+3x)+3`
`= 2x^2+3`
`Q(x)=`\(3x^2-3x+2-x^3+2x-x^2\)
`= -x^3+(3x^2-x^2)+(-3x+2x)+2`
`= -x^3+2x^2-x+2`
`P(x)-Q(x)-R(x)=0`
`-> P(X)-Q(x)=R(x)`
`-> R(x)=P(x)-Q(x)`
`-> R(x)=(2x^2+3)-(-x^3+2x^2-x+2)`
`-> R(x)=2x^2+3+x^3-2x^2+x-2`
`= x^3+(2x^2-2x^2)+x+(3-2)`
`= x^3+x+1`
`@`\(\text{dn inactive.}\)
18 tháng 4 2023
a: P(x)-Q(x)-R(x)=0
=>R(x)=P(x)-Q(x)
=2x^2+3+x^3-2x^2+x-2
=x^3+x+1
PT
1
CM
22 tháng 12 2017
Hệ số của lũy thừa bậc 5 là 6
Hệ số của lũy thừa bậc 3 là – 4
Hệ số của lũy thừa bậc 2 là 9
Hệ số của lũy thừa bậc 1 là – 2
Hệ số của lũy thừa bậc 0 là 2
CM
23 tháng 6 2017
Chọn C
Ta có: P(x) + Q(x) = x3+ x2+ 2x-1
⇒ Q(x) = (x3 + x2 + 2x-1) - P(x)
= 2x3 + 4x2 - 8x - 3.
22 tháng 6 2023
a: f(0)=0+0-0+3=3
=>x=0 ko là nghiệm của f(x)
g(0)=0+0+0+1=1
=>x=0 ko là nghiệm của g(x)
b: f(x)+g(x)
=x^3+4x^2-5x+3+x^3+3x^2-2x+1
=2x^3+7x^2-7x+4
c: f(x)-g(x)
=x^3+4x^2-5x+3-x^3-3x^2+2x-1
=x^2-3x+2
TH
2
5 tháng 3 2022
\(A=5x^3-7x^2+3x^3-4x^2+x^2-x^3+5x-1=7x^3-10x^2+5x-1\)
\(B=5x^3+3x^2-7x^4-5x^3+4x^2-x^4+3=-8x^4+7x^2+3\)
28 tháng 4 2023
a: \(=\dfrac{x^3-3x^2-7x+x^2-3x-7}{x^2-3x-7}=x+1\)
b:\(=\dfrac{x^3+x^2+3x^2+3x+5x+5}{x+1}=x^2+3x+5\)
c:\(=\dfrac{x^3-3x^2-7x+2x^2-6x-14}{x^2-3x-7}=x+2\)
d: \(=\dfrac{x^2\left(x+5\right)+5x+25-25}{x+5}=x^2+5-\dfrac{25}{x+5}\)
23 tháng 3 2022
a.\(P\left(x\right)=1+3x^5-4x^2+x^5+x^3-x^2+3x^3\)
\(=1-5x^2+4x^3+4x^5\)
\(Q\left(x\right)=2x^5-x^2+4x^5-x^4+4x^2-5x\)
\(=-5x+3x^2+3x^4+2x^5\)
b.\(P\left(x\right)+Q\left(x\right)=1-5x^2+4x^3+4x^5-5x+3x^2+3x^4+2x^5\)
\(=6x^5+3x^4+4x^3-2x^2-5x+1\)
\(P\left(x\right)-Q\left(x\right)=1-5x^2+4x^3+4x^5+5x-3x^2-3x^4-2x^5\)
\(=2x^5-3x^4+4x^3-8x^2+5x+1\)
c.\(P\left(x\right)+Q\left(x\right)=6x^5+3x^4+4x^3-2x^2-5x+1\)
\(x=-1\)
\(P\left(x\right)+Q\left(x\right)=6.\left(-1\right)^5+3.\left(-1\right)^4+4.\left(-1\right)^3-5.\left(-1\right)+1\)
\(=-6+3-4+5+1=-1\)
d.\(Q\left(0\right)=\)\(-5x+3x^2+3x^4+2x^5\)
\(=0\)
\(P\left(0\right)=\)\(1-5x^2+4x^3+4x^5\)
\(=1\)
Vậy x=0 ko là nghiệm của đa thức P(x)
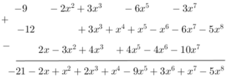
sửa đề
\(\left(4x^2-1\right)\left(x^3+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x^2-1=0\\x^3+8=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=\dfrac{1}{4}\\x^3=-8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\dfrac{1}{2}\\x=-2\end{matrix}\right.\)