K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DL
29 tháng 9 2019
\(A=2\sqrt{1}+2\sqrt{3}+...+2\sqrt{21}\)
\(A=2.\left(\sqrt{1}+\sqrt{3}+...+\sqrt{21}\right)\)
\(B=2\sqrt{2}+2\sqrt{4}+....2\sqrt{22}\)
\(B=2.\left(\sqrt{2}+\sqrt{4}+...+\sqrt{22}\right)\)
Có \(\sqrt{1}+\sqrt{3}+...+\sqrt{21}\) Có 11 số hạng.
\(\sqrt{2}+\sqrt{4}+...+\sqrt{22}\) Có 11 số hạng.
Mà \(\hept{\begin{cases}\sqrt{1}< \sqrt{2}\\....\\\sqrt{21}< \sqrt{22}\end{cases}}\)
=> \(2.\left(\sqrt{1}+\sqrt{3}+...+\sqrt{21}\right)< 2.\left(\sqrt{2}+\sqrt{4}+...+\sqrt{22}\right)\)
\(\Rightarrow A< B\)
ST
5
17 tháng 6 2018
ko hỉu sao !
trên đời có nhìu người zai dữ ~
Haiz...
bị trừ điểm giờ !
3 tháng 8 2021
b) Ta có: \(B=3\sqrt{50}-7\sqrt{8}+12\sqrt{18}\)
\(=15\sqrt{2}-14\sqrt{2}+36\sqrt{2}\)
\(=37\sqrt{2}\)
c) Ta có: \(C=2\sqrt{80}-2\sqrt{245}+2\sqrt{180}\)
\(=8\sqrt{5}-14\sqrt{5}+12\sqrt{5}\)
\(=6\sqrt{5}\)
d) Ta có: \(D=2\sqrt{12}-\sqrt{48}+3\sqrt{27}-\sqrt{108}\)
\(=4\sqrt{3}-4\sqrt{3}+9\sqrt{3}-6\sqrt{3}\)
\(=3\sqrt{3}\)
H9
HT.Phong (9A5)
CTVHS
27 tháng 6 2023
a) \(\sqrt{1-4x+4x^2}=5\)
\(\Leftrightarrow\sqrt{\left(1-2x\right)^2}=5\)
\(\Leftrightarrow\left|1-2x\right|=5\)
\(\Leftrightarrow2x-1=5\)
\(\Leftrightarrow2x=6\)
\(\Leftrightarrow x=3\)
b) \(\sqrt{x^2+6x+9}=3x-1\)
\(\Leftrightarrow\sqrt{\left(x+3\right)^2=3x-1}\)
\(\Leftrightarrow\left|x+3\right|=3x-1\)
\(\Leftrightarrow x+3=3x-1\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\)
Y
27 tháng 6 2023
\(a,\sqrt{1-4x+4x^2}=5\\ \Leftrightarrow\sqrt{\left(1-2x\right)^2}=5\\ \Leftrightarrow\left|1-2x\right|=5\)
\(TH_1:x\le\dfrac{1}{2}\)
\(1-2x=5\\ \Leftrightarrow x=-2\left(tm\right)\)
\(TH_2:x\ge\dfrac{1}{2}\)
\(-1+2x=5\\ \Leftrightarrow x=3\left(tm\right)\)
Vậy \(S=\left\{-2;3\right\}\)
\(b,\sqrt{x^2+6x+9}=3x-1\\ \Leftrightarrow\sqrt{\left(x+3\right)^2}=3x-1\\ \Leftrightarrow\left|x+3\right|=3x-1\)
\(TH_1:x\ge-3\\ x+3=3x-1\\ \Leftrightarrow-2x=-4\Leftrightarrow x=2\left(tm\right)\)
\(TH_2:x< 3\\ -x-3=3x-1\\ \Leftrightarrow-4x=2\\ \Leftrightarrow x=-\dfrac{1}{2}\left(tm\right)\)
Vậy \(S=\left\{2;-\dfrac{1}{2}\right\}\)
AT
21 tháng 7 2021
a) \(\sqrt{-\dfrac{2t}{3}}.\sqrt{-\dfrac{3t}{8}}=\sqrt{-\dfrac{2t}{3}.\left(-\dfrac{3t}{8}\right)}=\sqrt{\dfrac{1}{4}t^2}=\left|\dfrac{1}{2}t\right|=-\dfrac{1}{2}t\left(t< 0\right)\)
b) \(\sqrt{\dfrac{2a^3}{b}}:\sqrt{\dfrac{ab^3}{8}}=\sqrt{\dfrac{2a^3}{b}:\dfrac{ab^3}{8}}=\sqrt{\dfrac{2a^3}{b}.\dfrac{8}{ab^3}}=\sqrt{16\dfrac{a^2}{b^4}}\)
\(=\left|4\dfrac{a}{b^2}\right|=-\dfrac{4a}{b^2}\left(a< 0\right)\)
c) \(\sqrt{x-\sqrt{x^2-1}}.\sqrt{x+\sqrt{x^2-1}}=\sqrt{\left(x-\sqrt{x^2-1}\right)\left(x+\sqrt{x^2-1}\right)}\)
\(=\sqrt{x^2-\left(x^2-1\right)}=\sqrt{1}=1\)
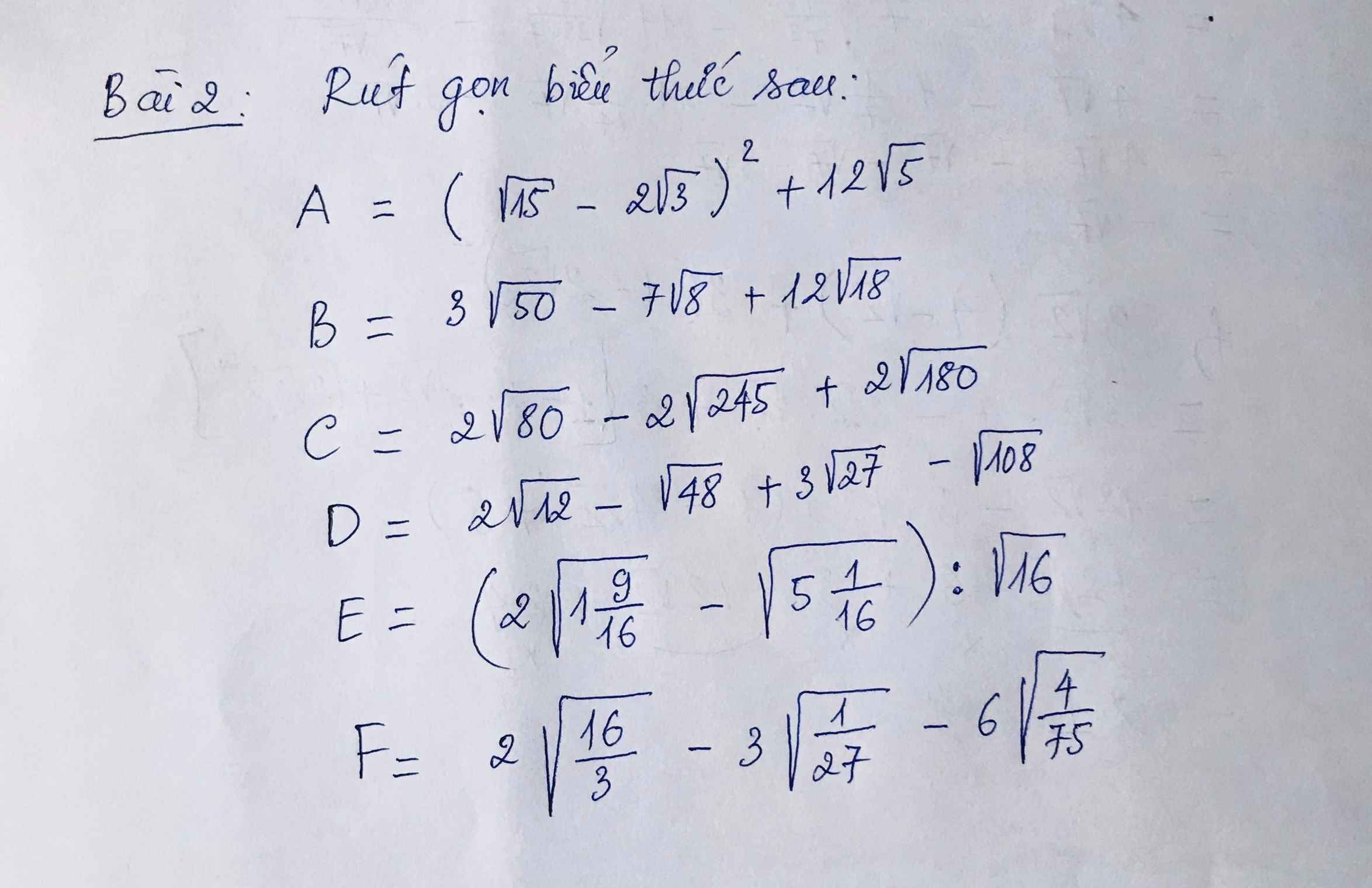
\(\sqrt{4x+1}-\sqrt{3x+4}=1\) ĐK : \(x\ge-\dfrac{1}{4}\)
\(\Leftrightarrow\left(\sqrt{4x+1}-\sqrt{3x+4}\right)^2=1\)
\(\Leftrightarrow4x+1-2\sqrt{\left(4x+1\right)\left(3x+4\right)}+3x+4=1\)
\(\Leftrightarrow2\sqrt{\left(4x+1\right)\left(3x+4\right)}=7x+4\)
\(\Leftrightarrow\sqrt{\left(4x+1\right)\left(3x+4\right)}=\dfrac{7x+4}{2}\)
\(\Leftrightarrow\left(4x+1\right)\left(3x+4\right)=\dfrac{49x^2+56x+16}{4}\)
\(\Leftrightarrow12x^2+19x+4=\dfrac{49x^2+56x+16}{4}\)
\(\Leftrightarrow48x^2+76x+16=49x^2+56x+16\)
\(\Leftrightarrow x^2-20x=0\)
\(\Leftrightarrow x\left(x-20\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=20\end{matrix}\right.\)
Mình không hiểu dấu tương đương thứ 5 bạn ạ! Bạn giúp mình đc k hì😍