Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{1}{2^2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{1.3}\)
\(...\)
\(\dfrac{1}{100^2}>\dfrac{1}{99.100}\)
\(\Rightarrow\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{99.100}\\ \Rightarrow\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}< \dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ \Rightarrow\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}< 1-\dfrac{1}{100}=\dfrac{99}{100}\\ \dfrac{99}{100}< \dfrac{1}{4}\\ \Rightarrowđpcm\)

a) \(\dfrac{5x-3}{3-2x}=\dfrac{2}{3}\)
\(\Rightarrow3\left(5x-3\right)=2\left(3-2x\right)\)
\(\Rightarrow15x-9=6-4x\)
\(\Rightarrow15x+4x=9+6\)
\(\Rightarrow19x=15\Rightarrow x=\dfrac{15}{19}\)
b) \(\left(\dfrac{4}{5}x+\dfrac{2}{3}\right):\dfrac{3}{4}=2\)
\(\Rightarrow\dfrac{4}{5}x+\dfrac{2}{3}=\dfrac{3}{2}\Rightarrow\dfrac{4}{5}x=\dfrac{5}{6}\)
\(\Rightarrow x=\dfrac{25}{24}\)
c) \(\dfrac{3}{4}x-\dfrac{1}{3}=\dfrac{3}{5}\Rightarrow\dfrac{3}{4}x=\dfrac{14}{15}\)
\(\Rightarrow x=\dfrac{56}{45}\)
d) \(\dfrac{2}{3}-\dfrac{3}{5}:x=\dfrac{1}{4}\Rightarrow\dfrac{3}{5}:x=\dfrac{5}{12}\)
\(\Rightarrow x=\dfrac{36}{25}\)

b) \(\dfrac{4}{5}-\dfrac{3}{4}:x=0,3\)
\(\Rightarrow0,8-0,75:x=0,3\)
\(\Rightarrow0,75:x=0,5\)
\(\Rightarrow x=1,5\)
c) \(\dfrac{-3}{2}-\dfrac{1}{4}x=1\dfrac{1}{3}-0,2x\)
\(\Rightarrow\dfrac{-3}{2}-\dfrac{4}{3}=\dfrac{1}{4}x-\dfrac{1}{5}x\)
\(\Rightarrow x=\dfrac{-17}{6}\cdot20\)
\(\Rightarrow x=\dfrac{-170}{3}\)

Ta có:
\(100-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}\right)=\dfrac{1}{2}+\dfrac{2}{3}+...+\dfrac{99}{100}\)
\(\Rightarrow100-1-\dfrac{1}{2}-...-\dfrac{1}{100}=\dfrac{1}{2}+\dfrac{2}{3}+...+\dfrac{99}{100}\)
\(\Rightarrow100=1+\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{2}{3}+...+\dfrac{1}{100}+\dfrac{99}{100}\)
\(\Rightarrow100=1+1+1+...+1\) (\(100\) số \(1\))
\(\Rightarrow100=100\)
Vậy \(100-\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}\right)=\dfrac{1}{2}+\dfrac{2}{3}+...+\dfrac{99}{100}\) (Đpcm)

a)\(\dfrac{2}{3}x-\dfrac{5}{6}=1\dfrac{1}{4}\)
\(\dfrac{2}{3}x-\dfrac{5}{6}=\dfrac{5}{4}\)
\(\dfrac{2}{3}x=\dfrac{5}{4}+\dfrac{5}{6}\)
\(\dfrac{2}{3}x=\dfrac{25}{12}\)
\(x=\dfrac{25}{12}:\dfrac{2}{3}\)
=>\(x=\dfrac{25}{8}\)
a) \(\dfrac{2}{3}x-\dfrac{5}{6}=1\dfrac{1}{4}\) b) \(2\dfrac{1}{3}-\dfrac{4}{5}:x=0,2\)
\(\dfrac{2}{3}x-\dfrac{5}{6}=\dfrac{5}{4}\) \(\dfrac{7}{3}-\dfrac{4}{5}:x=\dfrac{1}{5}\)
\(\dfrac{2}{3}x=\dfrac{5}{4}-\dfrac{5}{6}\) \(\dfrac{4}{5}:x=\dfrac{7}{3}-\dfrac{1}{5}\)
\(\dfrac{2}{3}x=\dfrac{30}{24}-\dfrac{20}{24}\) \(\dfrac{4}{5}:x=\dfrac{35}{15}-\dfrac{3}{15}\)
\(\dfrac{2}{3}x=\dfrac{5}{12}\) \(\dfrac{4}{5}:x=\dfrac{32}{15}\)
\(x=\dfrac{5}{12}:\dfrac{2}{3}\) \(x=\dfrac{4}{5}:\dfrac{32}{15}\)
\(x=\dfrac{5}{12}:\dfrac{8}{12}\) \(x=\dfrac{4}{5}.\dfrac{15}{32}\)
\(x=\dfrac{5}{12}.\dfrac{12}{8}=\dfrac{5}{8}\) \(x=\dfrac{4.15}{5.32}\)
\(x=\dfrac{1.3}{1.8}=\dfrac{3}{8}\)
d)\(\left(\dfrac{4}{3}-\dfrac{1}{4}x\right)^3=\dfrac{-8}{27}\)
\(\left(\dfrac{4}{3}-\dfrac{1}{4}x\right)^3=\left(\dfrac{-2}{3}\right)^3\)
\(\Rightarrow\dfrac{4}{3}-\dfrac{1}{4}x=\dfrac{-2}{3}\)
\(\Rightarrow\dfrac{1}{4}x=\dfrac{4}{3}-\dfrac{-2}{3}\)
\(\Rightarrow\dfrac{1}{4}x=2\)
\(\Rightarrow x=2:\dfrac{1}{4}\)
\(\Rightarrow x=2.4=8\)

Ta có :
\(A=\dfrac{1}{5^2}+\dfrac{2}{5^3}+\dfrac{3}{5^4}+.............+\dfrac{n}{5^{n+1}}+.....+\dfrac{11}{5^{12}}\)
\(\Rightarrow5A=\dfrac{1}{5}+\dfrac{2}{5^2}+\dfrac{3}{3^3}+........+\dfrac{n}{5^n}+..........+\dfrac{11}{5^{11}}\)
\(\Rightarrow5A-A=\left(\dfrac{1}{5}+\dfrac{2}{5^2}+\dfrac{3}{5^3}+.....+\dfrac{n}{5^n}+....+\dfrac{11}{5^{11}}\right)-\left(\dfrac{1}{5^2}+\dfrac{2}{5^3}+.....+\dfrac{n}{5^{n+1}}+........+\dfrac{11}{5^{12}}\right)\)\(\Rightarrow4A=\dfrac{1}{5}+\dfrac{1}{5^2}+........+\dfrac{1}{5^{11}}-\dfrac{11}{5^{12}}\)
\(\Rightarrow20A=1+\dfrac{1}{5}+.........+\dfrac{1}{5^{10}}-\dfrac{11}{5^{11}}\)
\(\Rightarrow20A-4A=\left(1+\dfrac{1}{5}+.......+\dfrac{1}{5^{10}}-\dfrac{11}{5^{11}}\right)-\left(\dfrac{1}{5}+\dfrac{1}{5^2}+........+\dfrac{1}{5^{11}}-\dfrac{11}{5^{12}}\right)\)\(\Rightarrow16A=1-\dfrac{12}{5^{11}}+\dfrac{11}{5^{12}}< 1\)
\(\Rightarrow A< \dfrac{1}{16}\rightarrowđpcm\)

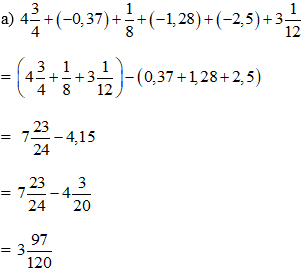
Bấm mt là ra mà bạn :v