Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Rút gọn:
\(\dfrac{-1}{6};\dfrac{1}{5};\dfrac{-1}{2}\)
Quy đồng:
\(\dfrac{-5}{30};\dfrac{6}{30};\dfrac{-15}{30}\)
b) Rút gọn:
\(\dfrac{-3}{5};\dfrac{-5}{8};\dfrac{-4}{9}\)
Quy đồng:
\(\dfrac{-216}{360};\dfrac{-225}{360};\dfrac{-160}{360}\)

a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)

a) \(\dfrac{-1}{2}\); \(\dfrac{-5}{3}\); \(\dfrac{-3}{4}\)
b)\(\dfrac{-6}{12}\); \(\dfrac{-20}{12}\); \(\dfrac{-9}{12}\)

\(\dfrac{3\cdot4+3\cdot7}{6\cdot5+9}=\dfrac{3\cdot11}{30+9}=\dfrac{33}{39}=\dfrac{11}{13}=\dfrac{77}{91}\)
\(\dfrac{6\cdot9-2\cdot17}{63\cdot3-119}=\dfrac{54-34}{189-119}=\dfrac{20}{70}=\dfrac{2}{7}=\dfrac{26}{91}\)

a) \(\dfrac{3}{8}\) và \(\dfrac{5}{27}\)
Mẫu số chung là 216
Quy đồng:
\(\dfrac{3.27}{8.27}\)=\(\dfrac{81}{216}\) ; \(\dfrac{5.8}{27.8}\)=\(\dfrac{40}{216}\)
b)\(\dfrac{-2}{9}\) và \(\dfrac{4}{25}\)
Mẫu số chung là:225
Quy đồng:
\(\dfrac{-2.25}{9.25}\)=\(\dfrac{-50}{225}\) ; \(\dfrac{4.9}{25.9}\)=\(\dfrac{36}{225}\)
c)\(\dfrac{1}{15}\) và -6
Mẫu số chung là 15
Quy đồng:
\(\dfrac{1}{15}\) ;\(\dfrac{-6.15}{15}\)=\(\dfrac{-90}{15}\)


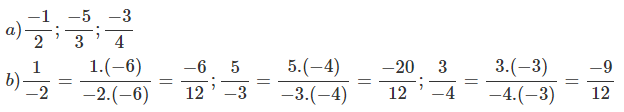
a. \(\dfrac{1}{5}\) đã tối giản
\(\dfrac{4}{120}=\dfrac{1}{30}\)
\(\dfrac{-50}{60}=\dfrac{-5}{6}\)
Quy đồng: \(BCNN\left(5,30,6\right)=30\)
\(\Rightarrow\dfrac{1}{5}=\dfrac{1.6}{5.6}=\dfrac{6}{30};\dfrac{1}{30}=\dfrac{1.1}{30.1}=\dfrac{1}{30};\dfrac{-5}{6}=\dfrac{-5.5}{6.5}=\dfrac{-25}{30}\)
b. \(\dfrac{-25}{30}< \dfrac{1}{30}< \dfrac{6}{30}\)
a,\(\dfrac{4}{120}=\dfrac{1}{30};\dfrac{-50}{60}=\dfrac{-5}{6}\)
\(\dfrac{1}{5}=\dfrac{1.6}{5.6}=\dfrac{6}{30};\dfrac{1}{30};\dfrac{-5}{6}=\dfrac{-5.5}{6.5}=\dfrac{-25}{30}\)
b, Vì \(\dfrac{6}{30}>\dfrac{1}{30}>\dfrac{-25}{30}\) nên => \(\dfrac{4}{120}>\dfrac{1}{30}>\dfrac{-50}{60}\)