K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 11 2016
x^3+y^3=3xy-1
x^3+y^3-3xy+1=0
(x+y)^3-3xy(x+y)-3xy+1=0
(x+y+1)(x^2+2xy+y^2-x-y+1)-3xy(x+y+1)=0
(x+y+1)(x^2+2xy+y^2-x-y+1-3xy)=0
suy ra +)x+y+1=0.VÌ x,y thuộc N* nên x+y+1 khác 0
+)x^2-xy+y^2+1-x-y=0
2(x^2-xy+y^2+1-x-y)=0
2x^2-2xy+2y^2+2-2x-2y=0
(x^2-2xy+y^2)+(x^2-2x+1)+(y^2-2y+1)=0
(x-y)^2+(x-1)^2+(y-1)^2=0
suy ra +)x-y=0
+)x-1=0
+)y-1=0
Vậy x=y=1
NQ
1
LH
4
5 tháng 12 2016
Ta có vì x, y là các số tự nhiên nên
\(\hept{\begin{cases}3xy\ge0\left(1\right)\\2x\ge0\left(2\right)\\2y\ge0\left(3\right)\end{cases}}\)
Từ đó ta có
\(3xy+2x+2y\ge0\)
Dấu = xảy ra khi \(x=y=0\)
TQ
6
TQ
2
28 tháng 10 2016
3xy + 2x + 2y = 0
=> x.(3y + 2) = -2y
=> \(x=\frac{-2y}{3y+2}\)
Do \(x\in N\Rightarrow3y+2\inƯ\left(-2y\right)\)
Mà 3y + 2 > -2y do y ϵ N => -2y = 0
=> y = 0; x = 0
Vậy x = y = 0
MA
1
TC
1
AH
Akai Haruma
Giáo viên
24 tháng 9 2023
Lời giải:
a. $2y(3x-1)+9x-3=7$
$2y(3x-1)+3(3x-1)=7$
$(3x-1)(2y+3)=7$
Vì $3x-1, 2y+3$ đều là số nguyên với mọi $x,y\in N$, và $2y+3>0$ nên ta có bảng sau: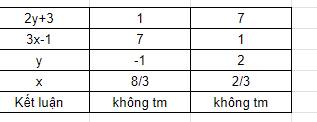
b.
$3xy-2x+3y-9=0$
$x(3y-2)+3y-9=0$
$x(3y-2)+(3y-2)-7=0$
$(3y-2)(x+1)=7$
Đến đây bạn cũng lập bảng tương tự như phần a.
Lời giải:
Giả sử $x,y$ là các số nguyên.
$3xy+2x+2y=0$
$x(3y+2)+2y=0$
$3x(3y+2)+6y=0$
$3x(3y+2)+2(3y+2)=4$
$(3x+2)(3y+2)=4$
Vì $x,y$ là các số nguyên nên ta xét bảng sau:
p/s: Lần sau bạn chú ý ghi đầy đủ yêu cầu của đề bài.