K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VM
23 tháng 2 2020
a) \(\left(5x^2-2x+10\right)^2=\left(3x^2+10x-8\right)^2\)
Vậy phương trình có tập hợp nghiệm là: \(S=\left\{3;-\frac{1}{2}\right\}.\)
b) \(\left(\frac{3x}{5}-\frac{1}{3}\right)^2=\left(\frac{x}{5}+\frac{2}{3}\right)^2\)
\(\Leftrightarrow\left(\frac{3x}{5}-\frac{1}{3}\right)^2-\left(\frac{x}{5}+\frac{2}{3}\right)^2=0\)
\(\Leftrightarrow\left(\frac{3x}{5}-\frac{1}{3}-\frac{x}{5}-\frac{2}{3}\right).\left(\frac{3x}{5}-\frac{1}{3}+\frac{x}{5}+\frac{2}{3}\right)=0\)
\(\Leftrightarrow\left(\frac{2x}{5}-1\right).\left(\frac{4x}{5}+\frac{1}{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\frac{2x}{5}-1=0\\\frac{4x}{5}+\frac{1}{3}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\frac{2x}{5}=1\\\frac{4x}{5}=-\frac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=1.5\\4x=\left(-\frac{1}{3}\right).5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=5\\4x=-\frac{5}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{5}{2}\\x=-\frac{5}{12}\end{matrix}\right.\)
Vậy phương trình có tập hợp nghiệm là: \(S=\left\{\frac{5}{2};-\frac{5}{12}\right\}.\)
Chúc bạn học tốt!
ND
11 tháng 12 2017
\(a.\)
\(\left(x^2-25\right):\dfrac{2x+10}{3x-7}\)
\(=\left(x-5\right)\left(x+5\right).\dfrac{3x-7}{2\left(x+5\right)}\)
\(=\dfrac{\left(x-5\right)\left(x+5\right)\left(3x-7\right)}{2\left(x+5\right)}\)
\(=\dfrac{\left(x-5\right)\left(3x-7\right)}{2}\)
\(b.\)
\(\dfrac{x^2+x}{5x^2-10x+5}:\dfrac{3x+3}{5x-5}\)
\(=\dfrac{x\left(x+1\right)}{5\left(x^2-2x+1\right)}.\dfrac{5\left(x-1\right)}{3\left(x+3\right)}\)
\(=\dfrac{x\left(x+1\right)}{5\left(x-1\right)^2}.\dfrac{5\left(x-1\right)}{3\left(x+1\right)}\)
\(=\dfrac{x\left(x+1\right).5\left(x-1\right)}{5\left(x-1\right)^2.3\left(x+1\right)}\)
\(=\dfrac{x}{3\left(x-1\right)}\)
NH
11 tháng 12 2017
\(\dfrac{x^2+x}{5x^2-10x+5}:\dfrac{3x+3}{5x-5}=\dfrac{5x\left(x+1\right)\left(x-1\right)}{15\left(x-1\right)^2\left(x+1\right)}=\dfrac{x}{3\left(x-1\right)}\)\(\left(x^2-25\right):\dfrac{2x+10}{3x-7}=\dfrac{\left(x-5\right)\left(x+5\right)\left(3x-7\right)}{2\left(x+5\right)}=\dfrac{\left(x-5\right)\left(3x-7\right)}{2}\)
3 tháng 7 2017
a, \(\left(x^2-y^2\right)-\left(5x+5y\right)\)
\(=\left(x-y\right)\left(x+y\right)-5\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-5\right)\)
b, \(5x^3-5x^2y-10x^2+10xy\)
\(=5x^2\left(x-y\right)-10x\left(x-y\right)\)
\(=\left(5x-10x\right)\left(x-y\right)=5x\left(x-2\right)\left(x-y\right)\)
c, \(2x^2-5x=x\left(2x-5\right)\)
f, \(3x^2-7x-10=3x^2+3x^2-10x-10\)
\(=3x^2\left(x+1\right)-10\left(x+1\right)=\left(3x^2-10\right)\left(x+1\right)\)
d, \(x^3-3x^2+1-3x=x^3-3x^2-3x+1\)
\(=x^3+x^2-4x^2-4x+x+1\)
\(=x^2\left(x+1\right)-4x\left(x+1\right)+\left(x+1\right)\)
\(=\left(x^2-4x+1\right)\left(x+1\right)\)
e, \(3x^2-6xy+3y^2-12z^2\)
\(=3\left(x^2-2xy+y^2-4z^2\right)\)
\(=3\left[\left(x-y\right)^2-4z^2\right]\)
\(=3\left(x-y-2z\right)\left(x-y+2z\right)\)
g, \(x^4+1-2x^2=\left(x^2-1\right)^2\)
h, \(3x^2-3y^2-12x+12y=3\left(x^2-y^2\right)-12\left(x-y\right)\)
\(=3\left(x-y\right)\left(x+y\right)-12\left(x-y\right)\)
\(=\left(x-y\right)\left(3x+3y-12\right)\)
\(=3\left(x-y\right)\left(x+y-4\right)\)
j, \(x^2-3x+2=x^2-2x-x+2=x\left(x-2\right)-\left(x-2\right)\)
\(=\left(x-1\right)\left(x-2\right)\)
3 tháng 7 2017
a. \(\left(x^2-y^2\right)-5\left(x+y\right)\)
\(=\left(x-y\right)\left(x+y\right)-5\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-5\right)\)
b. \(5x^3-5x^2y-10x^2+10xy\)
\(=5\left[\left(x^3-x^2y\right)-\left(2x^2-2xy\right)\right]\)
\(=5\left[x^2\left(x-y\right)-2x\left(x-y\right)\right]\)
\(=5x\left(x-y\right)\left(x-2\right)\)
c. \(2x^2-5x=x\left(2x-5\right)\)
d. \(x^3-3x^2+1-3x\)
\(=\left(x^3+1\right)-\left(3x^2+3x\right)\)
\(=\left(x+1\right)\left(x^2-x+1\right)-3x\left(x+1\right)\)
\(=\left(x+1\right)\left[x^2-x+1-3x\right]\)
\(=\left(x+1\right)\left[x^2-4x+1\right]\)
\(=\left(x+1\right)\left[x^2-2.x.2+2^2-2^2+1\right]\)
\(=\left(x+1\right)\left[\left(x-2\right)^2-3\right]\)
\(=\left(x+1\right)\left(x-2+\sqrt{3}\right)\left(x-2-\sqrt{3}\right)\)
e. \(3x^2-6xy+3y^2-12z^2\)
\(=3\left[x^2-2xy+y^2-4z^2\right]\)
\(=3\left[\left(x-y\right)^2-\left(2z\right)^2\right]\)
\(=3\left(x-y+2z\right)\left(x-y-2z\right)\)
f. \(3x^2-7x-10\)
\(=3x^2-7x-7-3\)
\(=\left(3x^2-3\right)-\left(7x+7\right)\)
\(=3\left(x^2-1\right)-7\left(x+1\right)\)
\(=3\left(x+1\right)\left(x-1\right)-7\left(x+1\right)\)
\(=\left(x+1\right)\left[3\left(x-1\right)-7\right]\)
\(=\left(x+1\right)\left(3x-8\right)\)
g. \(x^4+1-2x^2=\left(x^2\right)^2-2.x^2+1=\left(x^2-1\right)^2\)
\(=\left(x+1\right)^2\left(x-1\right)^2\)
h. \(3x^2-3y^2-12x+12y\)
\(=3\left(x^2-y^2\right)-12\left(x-y\right)\)
\(=3\left(x-y\right)\left(x+y\right)-12\left(x-y\right)\)
\(=\left(x-y\right)\left[3\left(x+y\right)-12\right]\)
\(=\left(x-y\right).3.\left(x+y-4\right)\)
j. \(x^2-3x+2=x^2-x-2x+2\)
\(=x\left(x-1\right)-2\left(x-1\right)\)
\(=\left(x-1\right)\left(x-2\right)\)
P/s: ( Có j sai ns nha nhiều số quá tui rối đầu )
26 tháng 3 2020
(3x2 + 10x - 8)2 = (5x2 - 2x + 10)2
<=> (3x2 + 10x - 8)2 - (5x2 - 2x + 10)2 = 0
<=> (3x2 + 10x - 8 - 5x2 + 2x - 10)(3x2 + 10x - 8 + 5x2 - 2x + 10) = 0
<=> (-2x2 + 12x - 18)(8x2 + 8x + 2) = 0
<=> -4(x2 - 6x + 9)(4x2 + 4x + 1) = 0
<=> (x - 3)2(2x + 1)2 = 0
<=> \(\orbr{\begin{cases}x-3=0\\2x+1=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=3\\x=-\frac{1}{2}\end{cases}}\)
Vậy S = {3; -1/2}
10 tháng 2 2018
a) \(\left(3x^2+10x-8\right)^2=\left(5x^2-2x+10\right)^2\)
\(3x^2+10x-8=5x^2-2x+10\)
\(3x^2-5x^2+10x+2x-8-10=0\)
\(-2x^2+12x-18=0\)
\(x^2-6x+9=0\)
\(\left(x-3\right)^2=0\)
\(\Rightarrow x-3=0\)
\(\Rightarrow x=3\)
b) \(\frac{x^2-x-6}{x-3}=0\)
\(\Rightarrow x^2-x-6=0\)
\(\Rightarrow x^2-2x.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}-6=0\)
\(\Rightarrow\left(x-\frac{1}{2}\right)^2-\frac{25}{4}=0\)
\(\Rightarrow\left(x-\frac{1}{2}-\frac{5}{2}\right)\left(x-\frac{1}{2}+\frac{5}{2}\right)=0\)
\(\Rightarrow\left(x-3\right)\left(x+2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-3=0\\x+2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=3\\x=-2\end{cases}}\)
30 tháng 12 2018
a) \(x^3-2x^2-5x+6=0\)
\(x^3-x^2-x^2+x-6x+6=0\)
\(x^2\left(x-1\right)-x\left(x-1\right)-6\left(x-1\right)=0\)
\(\left(x-1\right)\left(x^2-x-6\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-1=0\\x^2-x-6=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=1\\x^2-2x+3x-6=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=1\\\left(x+3\right)\left(x-2\right)=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=1\\x=\left\{2;-3\right\}\end{cases}}\)
30 tháng 12 2018
\(a,x^3-2x^2-5x+6=0\)
\(\Leftrightarrow\left(x^3-x^2\right)-\left(x^2-x\right)-\left(6x-6\right)=0\)
\(\Leftrightarrow x^2\left(x-1\right)-x\left(x-1\right)-6\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-x-6\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[\left(x^2-3x\right)+\left(2x-6\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left[x\left(x-3\right)+2\left(x-3\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x-3\right)=0\)
\(\Leftrightarrow x-1=0\left(h\right)x+2=0\left(h\right)x-3=0\)
\(\Leftrightarrow x=1\left(h\right)x=-2\left(h\right)x=3\)
Vậy \(x\in\left\{-2;1;3\right\}\)
P/S: (h) là hoặc nhé
23 tháng 2 2019
Câu 2:
ĐKXĐ: \(\left[{}\begin{matrix}1-9x^2\ne0\\1+3x\ne0\\1-3x\ne0\end{matrix}\right.\Rightarrow \left[{}\begin{matrix}x\ne\dfrac{-1}{3}\\x\ne\dfrac{1}{3}\end{matrix}\right.\)
\(\dfrac{12}{1-9x^2}=\dfrac{1-3x}{1+3x}-\dfrac{1+3x}{1-3x}\left(1\right)\)
\(\left(1\right):\dfrac{12}{\left(1-3x\right)\left(1+3x\right)}-\dfrac{\left(1-3x\right)\left(1-3x\right)}{\left(1-3x\right)\left(1+3x\right)}+\dfrac{\left(1+3x\right)\left(1+3x\right)}{\left(1-3x\right)\left(1+3x\right)}=0\)
\(\Leftrightarrow 12-\left(1-3x-3x+9x^2\right)+\left(1+3x+3x+9x^2\right)=0\)
\(\Leftrightarrow 12-1+3x+3x-9x^2+1+3x+3x+9x^2=0\)
\(\Leftrightarrow12x+12=0\\ \Leftrightarrow12x=-12\\ \Leftrightarrow x=-1\left(TM\right)\)
Vậy \(S=\left\{-1\right\}\)
19 tháng 7 2016
\(a,\frac{3}{2x+6}-\frac{x-6}{2x^2+6x}\) (x khác -3; khác 0)
\(=\frac{3}{2\left(x+3\right)}-\frac{x-6}{2x.\left(x+3\right)}=\frac{3x}{2x.\left(x+3\right)}-\frac{x-6}{2x.\left(x+3\right)}=\frac{3x-x+6}{2x.\left(x+3\right)}=\frac{2x+6}{x.\left(2x+6\right)}=\frac{1}{x}\)
19 tháng 7 2016
\(b,\left(\frac{2x+1}{2x-1}-\frac{2x-1}{2x+1}\right):\frac{4x}{10x-5}\) (x khác 0 , khác 1/2 khác -1/2 )
\(=\left(\frac{\left(2x+1\right)^2}{\left(2x-1\right)\left(2x+1\right)}-\frac{\left(2x-1\right)^2}{\left(2x-1\right)\left(2x+1\right)}\right).\frac{10x-5}{4x}\)
\(=\left(\frac{4x^2+4x+1}{\left(2x-1\right)\left(2x+1\right)}-\frac{4x^2-4x+1}{\left(2x-1\right)\left(2x+1\right)}\right).\frac{10x-5}{4x}\)
\(=\frac{8x}{\left(2x-1\right)\left(2x+1\right)}.\frac{5.\left(2x-1\right)}{4x}=\frac{10}{2x+1}\)
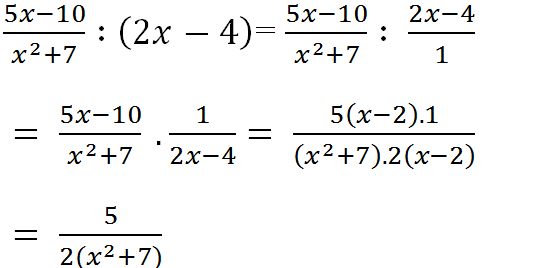
`(3x^2+10x-8)=(5x^2-2x+10)^2`
`<=>(3x^2+10x-8+5x^2-2x+10)(3x^2+10x-8-5x^2+2x-10)=0`
`<=> (8x^2+8x+2)(-2x^2+12x-18)=0`
\(\Leftrightarrow\left[{}\begin{matrix}8x^2+8x+2=0\\-2x^2+12x-18=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=3\end{matrix}\right.\)
Vậy `S={-1/2 ; 3}`.