Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\left(3sinx-4cosx\right)^2-2\left(3sinx-4cosx\right)\le2m-1\)
Đặt \(3sinx-4cosx=5\left(\frac{3}{5}sinx-\frac{4}{5}cosx\right)=5sin\left(x-a\right)=t\)
\(\Rightarrow-5\le t\le5\)
BPT trở thành: \(t^2-2t+1\le2m\)
\(\Leftrightarrow\left(t-1\right)^2\le2m\)
Để pt nghiệm đúng với mọi x thì \(2m\ge\max\limits_{\left[-5;5\right]}\left(t-1\right)^2\)
Mà \(\left(t-1\right)^2\le\left(-5-1\right)^2=36\)
\(\Rightarrow2m\ge36\Rightarrow m\ge18\)
Có \(2019-18+1=2002\) giá trị
Không đáp án nào đúng

Đáp án D
Đặt t = 3sin x - 4cos x => -5 ≤ t ≤ 5 (dùng bất đẳng thức bunhiacopxki)
Ta có: y = (3sin x – 4cos x)2 – 6sin x + 8cos x
= t2 – 2t = (t – 2)2 -1
Do -5 ≤ t ≤ 5 => 0 ≤ (t – 2)2 ≤ 36 => min y = -1
Suy ra yêu cầu bài toán -1 ≥ 2m - 1 ⇔ m ≤ 0.

ĐKXĐ: \(cosx\ne\frac{3}{4}\)
\(\Leftrightarrow3sinx+m=8cosx-6\)
\(\Leftrightarrow3sinx-8cosx=-m-6\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(3^2+8^2\ge\left(-m-6\right)^2\)
\(\Rightarrow\left(m+6\right)^2\le73\)
\(\Rightarrow-6-\sqrt{73}\le m\le-6+\sqrt{73}\)
Kết hợp thêm điều kiện \(m\ne12\pm\frac{3\sqrt{7}}{4}\)

Lời giải:
Đặt \(3\sin x+4\cos x=t\)
Áp dụng BĐT Bunhiacopxky:
\(t^2=(3\sin x+4\cos x)^2\leq (3^2+4^2)(\sin ^2x+\cos ^2x)=25\)
\(\Rightarrow -5\leq t\leq 5\)
Với $t\in [-5;5]$ ta có:
\(y=3t^2+4t+1\leq 3.25+4.5+1=96\)
Mặt khác: \(y=3t^2+4t+1=3(t+\frac{2}{3})^2-\frac{1}{3}\)
\((t+\frac{2}{3})^2\geq 0, \forall t\in [-5;5]\Rightarrow y\geq -\frac{1}{3}\)
Vậy \(y_{\min}=\frac{-1}{3}; y_{\max}=96\)

\(y'=3cosx-4sinx-\frac{1}{cos^2x}\)
\(\Rightarrow y'\left(\frac{\pi}{6}\right)=3cos\left(\frac{\pi}{6}\right)-4sin\left(\frac{\pi}{6}\right)-\frac{1}{cos^2\left(\frac{\pi}{6}\right)}=\frac{-20+9\sqrt{3}}{6}\)
b/ \(y'=-8x^3+\frac{3}{x^4}-\frac{1}{x^2}\)

1.
\(y=2\left(\frac{1}{2}sinx-\frac{\sqrt{3}}{2}cosx\right)=2sin\left(x-\frac{\pi}{3}\right)\)
\(sin\left(x-\frac{\pi}{3}\right)\le1\) ;\(\forall x\Rightarrow y\le2\) ;\(\forall x\)
\(y_{max}=2\) khi \(sin\left(x-\frac{\pi}{3}\right)=1\)
2.
\(y=5\left(\frac{3}{5}sinx+\frac{4}{5}cosx\right)\)
Đặt \(\frac{3}{5}=cosa\) với \(a\in\left(0;\pi\right)\)
\(\Rightarrow y=5\left(sinx.cosa+cosx.sina\right)=5sin\left(x+a\right)\)
\(-1\le sin\left(x+a\right)\le1\Rightarrow-5\le y\le5\)
\(y_{min}=-5\) ; \(y_{max}=5\)

Cái đoạn theo điều kiện có nghiệm sao lại suy ra được thế kia hả anh?
Tồn tại x để \(a.sinx+b.cosx=c\) khi và chỉ khi \(a^2+b^2\ge c^2\)
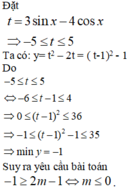
Đặt \(a=3sinx-4cosx\Rightarrow a^2\le\left(3^2+4^2\right)\left(sin^2x+cos^2x\right)=25\)
\(\Rightarrow-5\le a\le5\)
\(y=a^2-2a+1\ge2m\)
\(\Rightarrow\left(a-1\right)^2\ge2m\)
Để BPT đúng với mọi x thuộc R
\(\Leftrightarrow2m\le\min\limits_{\left[-5;5\right]}\left(a-1\right)^2\)
Mà \(\left(a-1\right)^2\ge0\) \(\forall a\Rightarrow2m\le0\Rightarrow m\le0\)