K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DD
8 tháng 4 2017
Bài 1 :
a , x = 675
b , x = 1764
c , x = 0
Bài 2 :
a , x = 3 , 2 , 1 , 0
b , x = 6 , 5 , 4 , 3 , 2 , 1 , 0
c , x = 3 , 4
4 tháng 4 2017
Bài 1:Tìm x
a, x:5=27\(x\)5
x:5=135
x =135\(x\)5
x =675
b, x:7=36\(x\)7
x:7=252
x =252\(x\)7
x =1764
c,x\(x\)132=312 x (5-3-2)
x\(x\)132=312x0
x\(x\)132=0
x =0:132
x =0
T
15 tháng 3 2019
\(\frac{24}{35}:\frac{3}{4}=\frac{24}{35}\cdot\frac{4}{3}=\frac{96}{105}=\frac{32}{35}\)
Hk tốt
13 tháng 5 2019
\(a,\)\(x+x+2x=164\)
\(\Rightarrow4x=164\)
\(\Rightarrow x=41\)
XN
6
HQ
Hà Quang Minh
Giáo viên
9 tháng 12 2023
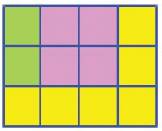
Hình chữ nhật có tất cả 12 ô vuông.
Có 2 ô vuông màu xanh. Đã tô $\frac{1}{6}$ số ô vuông của hình bằng màu xanh.
Có 4 ô vuông màu hồng. Đã tô $\frac{1}{3}$ số ô vuông của hình bằng màu hồng.
Có 6 ô vuông màu vàng. Đã tô $\frac{1}{2}$số ô vuông của hình bằng màu vàng.
SG
0
26 tháng 7 2020
chứng minh \(\frac{3}{2}\ge\frac{x}{1+x^2}+\frac{y}{1+y^2}+\frac{z}{1+z^2}\)
ta có \(\left(x-1\right)^2\ge0\Leftrightarrow x^2+1\ge2x\Leftrightarrow\frac{2x}{1+x^2}\le1\)
\(\left(y-1\right)^2\ge0\Leftrightarrow y^2+1\ge2y\Leftrightarrow\frac{2y}{1+y^2}\le1\)
\(\left(z-1\right)^2\ge0\Leftrightarrow z^2+1\ge2z\Leftrightarrow\frac{2z}{1+z^2}\le1\)
\(\Rightarrow\frac{2x}{1+x^2}+\frac{2y}{1+y^2}+\frac{2x}{1+z^2}\le3\Leftrightarrow\frac{x}{1+x^2}+\frac{y}{1+y^2}+\frac{z}{1+z^2}\le\frac{3}{2}\)
chứng minh \(\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}\ge\frac{3}{2}\)
áp dụng bất đẳng thức Cauchy ta có:
\(\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}\ge3\sqrt[3]{\frac{1}{\left(1+x\right)\left(1+y\right)\left(1+z\right)}}=\frac{3}{\sqrt{\left(1+x\right)\left(1+y\right)\left(1+z\right)}}\)
ta lại có \(\frac{\left(1+x\right)\left(1+y\right)\left(1+z\right)}{3}\ge\sqrt[3]{\left(1+x\right)\left(1+y\right)\left(1+z\right)}\)
vậy \(\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}\ge\frac{3}{\frac{\left(1+x\right)+\left(1+y\right)+\left(1+z\right)}{3}}=\frac{3}{2}\)
kết hợp ta có \(\frac{x}{1+x^2}+\frac{y}{1+y^2}+\frac{z}{1+z^2}\le\frac{3}{2}\le\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}\)
\(\dfrac{35}{2}\)=17.5
\(\dfrac{35}{1}x\dfrac{1}{2}=\dfrac{35}{2}\)