TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DX
1
NB
2
5 tháng 4 2016
S = 1x2 + 2x3 + 3x4 + ……………… + 11x12 + 12x13
3S=1x2x3 + 2x3x3 + 3x4x3+ ………. + 11x12x3 + 12x13x3
Ta lấy K = 1x2x3 +2x3x4 + 3x4x5 + …… + 11x12x13 + 12x13x14
- 3S = 1x2x3 + 2x3x3 + 3x4x3+ ……… + 11x12x3 + 12x13x3
------------------------------------------------------------------------------------
K – 3S = 0 + 2x3x1 + 3x4x2 + …… .. + 11x12x10 + 12x13x11
K – 3S = K – 12x13x14
Từ đó suy ra: 3S = 12x13x14
S = 4x13x14 = 728
Cách 2:
S x 3 = 1x2x3 + 2x3x(4-1) + 3x4x(5-2) + …. + 11x12x(13-10) + 12x13x(14-11)
S x 3 = 1x2x3 + 2x3x4 – 2x3x1 + 3x4x5 – 3x4x2 + …..+ 11x12x13 – 11x12x10 +12x13x14 – 12x13x11
S x 3 = 12 x 13 x14
S = 4 x 13 x 14
S = 728
ai k minh minh k lai cho
TM
19 tháng 6 2016
Đặt A=1x2+2x3+3x4+...+2016x2017
=>3A=3x1x2+3x2x3+3x3x4+...+3x2016x2017
=>3A=(3-0)x1x2+(4-1)x2x3+(5-2)x3x4+...+(2018-2015)x2016x2017
=>3A=1x2x3-0x1x2+2x3x4-1x2x3+3x4x5-2x3x4+...+2016x2017x2018-2015x2016x2017
=>3A=2016x2017x2018
=>A=\(\frac{2016\times2017\times2018}{3}\)(tự tính nha)
19 tháng 6 2016
S = 1x2 + 2x3 + 3x4 + 4x5 + ... + 2016x2017
3S = 1x2x3 + 2x3x(4-1) + 3x4x(5-2) + 4x5x(6-3) + ... + 2016x2017x(2018-2015)
3S = 1x2x3 + 2x3x4 - 1x2x3 + 3x4x5 - 2x3x4 + 4x5x6 - 3x4x5 + ... + 2016x2017x2018 - 2015x2016x2017
3S = 2016x2017x2018
S = 1/3 x 2016x2017x2018.
HN
12
NC
2
7 tháng 8 2016
A = 1 x 2 + 2 x 3 + 3 x 4 + ... + 99 x 100
3A = 1 x 2 x (3 - 0) + 2 x 3 x (4 - 1) + 3 x 4 x (5 - 2) + ... + 99 x 100 x (101 - 98)
3A = 1 x 2 x 3 - 0 x 1 x 2 + 2 x 3 x 4 - 1 x 2 x 3 + 3 x 4 x 5 - 2 x 3 x 4 + ... + 99 x 100 x 101 - 98 x 99 x 100
3A = (1 x 2 x 3 + 2 x 3 x 4 + 3 x 4 x 5 + ... + 99 x 100 x 101) - (0 x 1 x 2 + 1 x 2 x 3 + 2 x 3 x 4 + ... + 98 x 99 x 100)
3A = 99 x 100 x 101
A = 33 x 100 x 101
A = 333300
7 tháng 8 2016
A = 1x2+2x3+3x4+4x5+....+99x100
3A=1x2x(3-0)+2x3x(4-1)+3x4x(5-2)+...+99x100x(101-98)
3A= 1x2x3-0x1x2+2x3x4-1x2x3+3x4x5-2x3x4+...+99x100x101-98x99x100
3A= 99x100x101
A=999900 : 3 = 333300
DD
0
PM
6
HM
12 tháng 8 2017
Gọi biểu thức trên là A, ta có :
A = 1x2 + 2x3 + 3x4 + 4x5 + ...+ 99x100
A x 3 = 1x2x3 + 2x3x3 + 3x4x3 + 4x5x3 + ... + 99x100x3
A x 3 = 1x2x3 + 2x3x(4-1) + 3x4x(5-2) + 4x5x(6-3) + ... + 99x100x(101-98)
A x 3 = 1x2x3 + 2x3x4 - 1x2x3 + 3x4x5 - 2x3x4 + 4x5x6 - 3x4x5 + ... + 99x100x101 - 98x99x100.
A x 3 = 99x100x101
A = 99x100x101 : 3
A = 333300
GT
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 6 2023
1 \(\times\) 2 \(\times\) 3 = 1 \(\times\) 2 \(\times\) 3
2 \(\times\) 3 \(\times\) 3 = 2 \(\times\) 3 \(\times\) ( 4 -1) = 2 \(\times\) 3 \(\times\) 4 - 1 \(\times\) 2 \(\times\) 3
3 \(\times\) 4 \(\times\) 3 = 3 \(\times\) 4 \(\times\) ( 5 -2) = 3 \(\times\) 4 \(\times\) 5 - 2 \(\times\) 3 \(\times\) 4
4 \(\times\) 5 \(\times\) 3 = 4 \(\times\) 5 \(\times\) ( 6- 3) = 4 \(\times\) 5 \(\times\) 6 - 3 \(\times\) 4 \(\times\) 5
..................................................................................
99\(\times\)100\(\times\)3 = 99\(\times\)100\(\times\)(101-98) =99\(\times\)100\(\times\)101 - 98\(\times\)99\(\times\)100
Cộng vế với vế ta được:
1\(\times\)2\(\times\)3 + 2\(\times\)3\(\times\)3 + 3\(\times\)4\(\times\)3+ ...+99\(\times\)100\(\times\)3 = 99\(\times\)100\(\times\)101
(1\(\times\)2 + 2\(\times\)3 + 3\(\times\)4 +...+99\(\times\)100)\(\times\)3 = 99\(\times\)100\(\times\)101
1\(\times\)2 + 2\(\times\)3 + 3\(\times\)4+...+99\(\times\)100 = (99 \(\times\)100 \(\times\)101):3
1\(\times\)2 + 2\(\times\)3 + 3\(\times\)4+...+99\(\times\)100 = 333 300
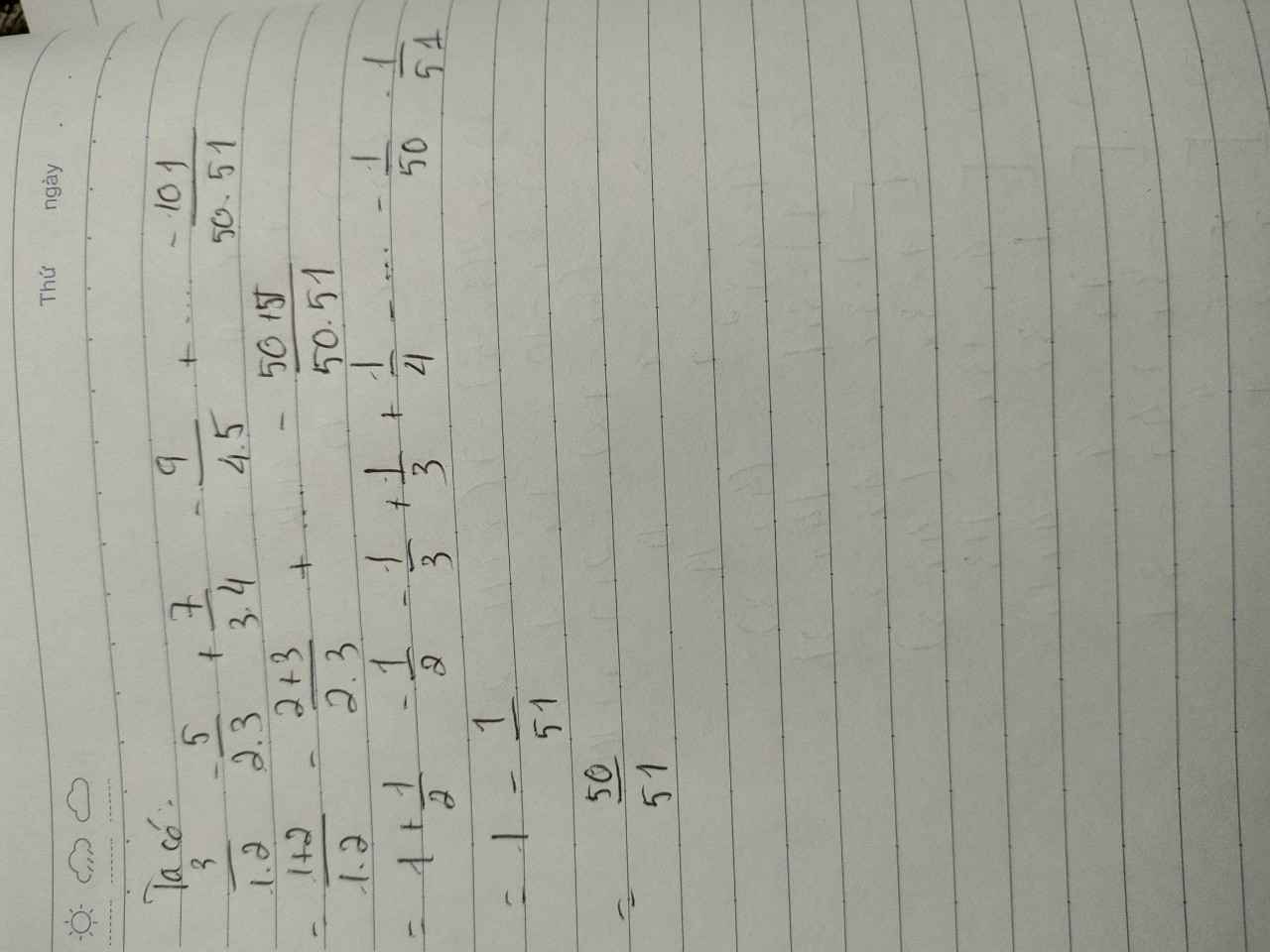
Ta có :
\(\dfrac{3}{1\times2}-\dfrac{5}{2\times3}+\dfrac{7}{3\times4}-\dfrac{9}{4\times5}+...-\dfrac{25}{12\times13}+\dfrac{27}{13\times14}\)
\(=\dfrac{2+1}{1\times2}-\dfrac{3+2}{2\times3}+\dfrac{4+3}{3\times4}-...+\dfrac{14+13}{13\times14}\)
\(=1+\dfrac{1}{2}-\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{4}-...+\dfrac{1}{13}+\dfrac{1}{14}\)
\(=1+\dfrac{1}{14}=\dfrac{15}{14}\)