Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn kiểm tra lại đề. Và vào hoc 24 để đăng nhé!
Làm câu cuối:
TXĐ: \(x\in\)[ 0 ; + vô cùng )
\(y'=\frac{1}{2\sqrt{x}}-1=0\Leftrightarrow2\sqrt{x}=1\Leftrightarrow x=\frac{1}{4}\left(tm\right)\)
Vẽ bảng biến thiên:
....
Từ bảng biên thiên:
Hàm số đồng biến trong khoảng ( 0 ; 1/4 )
Hàm số nghịch biên trong khoảng ( 1/4 ; + dương vô cùng)

a) Tập xác định : D = R { 1 }.
> 0, ∀x
1.
Hàm số đồng biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
b) Tập xác định : D = R { 1 }.
< 0, ∀x
1.
Hàm số nghịch biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
c) Tập xác định : D = (-∞ ; -4] ∪ [5 ; +∞).
∀x ∈ (-∞ ; -4] ∪ [5 ; +∞).
Với x ∈ (-∞ ; -4) thì y’ < 0; với x ∈ (5 ; +∞) thì y’ > 0. Vậy hàm số nghịch biến trên khoảng (-∞ ; -4) và đồng biến trên khoảng (5 ; +∞).
d) Tập xác định : D = R { -3 ; 3 }.
< 0, ∀x
±3.
Hàm số nghịch biến trên các khoảng : (-∞ ; -3), (-3 ; 3), (3 ; +∞).

Câu 1: Xét trên miền [1;4]
Do \(f\left(x\right)\) đồng biến \(\Rightarrow f'\left(x\right)\ge0\)
\(x\left(1+2f\left(x\right)\right)=\left[f'\left(x\right)\right]^2\Leftrightarrow x=\frac{\left[f'\left(x\right)\right]^2}{1+2f\left(x\right)}\Leftrightarrow\frac{f'\left(x\right)}{\sqrt{1+2f\left(x\right)}}=\sqrt{x}\)
Lấy nguyên hàm 2 vế:
\(\int\frac{f'\left(x\right)dx}{\sqrt{1+2f\left(x\right)}}=\int\sqrt{x}dx\Leftrightarrow\int\left(1+2f\left(x\right)\right)^{-\frac{1}{2}}d\left(f\left(x\right)\right)=\int x^{\frac{1}{2}}dx\)
\(\Leftrightarrow\sqrt{1+2f\left(x\right)}=\frac{2}{3}x\sqrt{x}+C\)
Do \(f\left(1\right)=\frac{3}{2}\Rightarrow\sqrt{1+2.\frac{3}{2}}=\frac{2}{3}.1\sqrt{1}+C\Rightarrow C=\frac{4}{3}\)
\(\Rightarrow\sqrt{1+2f\left(x\right)}=\frac{2}{3}x\sqrt{x}+\frac{4}{3}\)
Đến đây có thể bình phương chuyển vế tìm hàm \(f\left(x\right)\) chính xác, nhưng dài, thay luôn \(x=4\) vào ta được:
\(\sqrt{1+2f\left(4\right)}=\frac{2}{3}4.\sqrt{4}+\frac{4}{3}=\frac{20}{3}\Rightarrow f\left(4\right)=\frac{\left(\frac{20}{3}\right)^2-1}{2}=\frac{391}{18}\)
Câu 2:
Diện tích hình phẳng cần tìm là hai miền đối xứng qua Oy nên ta chỉ cần tính trên miền \(x\ge0\)
Hoành độ giao điểm: \(sinx=x-\pi\Rightarrow x=\pi\)
\(S=2\int\limits^{\pi}_0\left(sinx-x+\pi\right)dx=4+\pi^2\Rightarrow\left\{{}\begin{matrix}a=4\\b=1\end{matrix}\right.\)
\(\Rightarrow2a+b^3=9\)

a) Tập xác định : R ; y' =-4x3 + 16x = -4x(x2 - 4);
y' = 0 ⇔ x = 0, x = ±2 .
Bảng biến thiên :
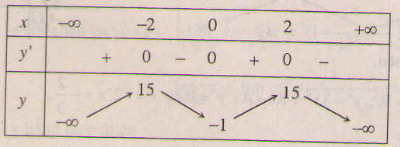
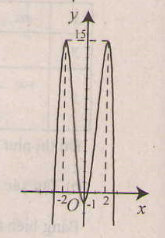
Đồ thị như hình bên.
b) Tập xác định : R ; y' =4x3 - 4x = 4x(x2 - 1);
y' = 0 ⇔ x = 0, x = ±1 .
Bảng biến thiên :
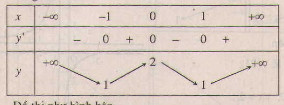
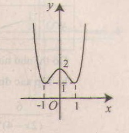
Đồ thị như hình bên.
c) Tập xác định : R ; y' =2x3 + 2x = 2x(x2 + 1); y' = 0 ⇔ x = 0.
Bảng biến thiên :
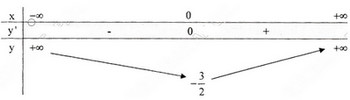
Đồ thị như hình bên.
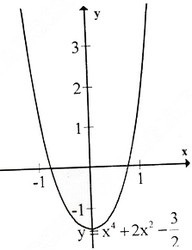
d) Tập xác định : R ; y' = -4x - 4x3 = -4x(1 + x2); y' = 0 ⇔ x = 0.
Bảng biến thiên :
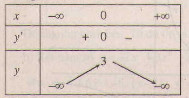
Đồ thị như hình bên.
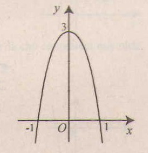 .
.

a) y′=6x2+6x−36=6(x2+x−6)y′=6x2+6x−36=6(x2+x−6)
y’= 0 ⇔ x2+ x – 6= 0 ⇔ x=2; x=-3
Bảng biến thiên :
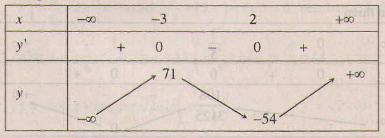
Hàm số đạt cực đại tại x = -3 , ycđ = y(-3) = 71
Hàm số đạt cực tiểu tại x = 2 , y(ct) = y(2) = -54
b) y’ = 4x3 + 4x = 4x(x2 + 1); y’ = 0 ⇔ x = 0.
Bảng biến thiên :
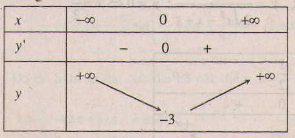
Hàm số đạt cực tiểu tại x = 0 , y(ct) = y(0) = -3
c) Tập xác định : D = R\{0}

Bảng biến thiên :
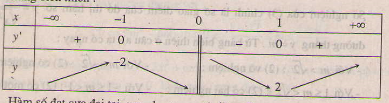
Hàm số đạt cực đại tại x = -1 , ycđ = y(-1) = -2 ;
Hàm số đạt cực tiểu tại x = 1 , yct = y(1) = 2.
d) Tập xác định : D = R.
y’ = 3x2(1 – x)2 + x3 . 2(1 – x)(-1) = x2 (1 – x)[3(1 – x) - 2x] = x2 (x – 1)(5x – 3) .
y’ = 0 ⇔ x = 0, x = , x = 1.
, x = 1.
Bảng biến thiên :
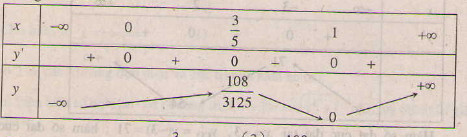
Hàm số đạt cực đại tại x =  , ycđ =
, ycđ =  =
=  ;
;
Hàm số đạt cực tiểu tại x = 1 , yct = y(1) = 0 .
e) Tập xác định : D = R. 
Hàm số đạt cực tiểu tại 

a) y′=3x+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0y′=3x2+2(m+3)x=x[3x+2(m+3)];y′=0⇔x1=0
hoặc x2=−2m+63x2=−2m+63
Xảy ra hai trường hợp đối với dấu của y':
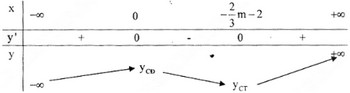
Rõ ràng, để hàm số có điểm cực đại tại x = -1 ta phải có
x2=−2m+63=−1⇔m=−32x2=−2m+63=−1⇔m=−32
(Chú ý : trường hợp x1 = x2 thì hàm số không có cực trị).
b) (Cm) cắt Ox tại x = -2 ⇔ -8 + 4(m + 3) + 1 - m = 0 ⇔ m=−53m=−53

Lời giải:
Đặt \(\log_yx=a,\log_xy=b\). Khi đó ta có:
\(\left\{\begin{matrix} a+b=\frac{10}{3}\\ ab=\log_xy.\log_yx=1\end{matrix}\right.\)
Áp dụng định lý Viete đảo thì \(a,b\) là nghiệm của PT:
\(x^2-\frac{10}{3}x+1=0\) . PT trên có hai nghiệm \(3,\frac{1}{3}\)
Giả sử \(a=\log_yx=3\) và \(b=\log_xy=\frac{1}{3}\)
\(\left\{\begin{matrix} \log_y\left(\frac{144}{y}\right)=3\\ \log_x\left(\frac{144}{x}\right)=\frac{1}{3} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x=24\sqrt{3}\\ y=2\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow \frac{x+y}{2}=13\sqrt{3}\). Đáp án D

Câu 1:
\(y=x^3-3x^2-2\Rightarrow y'=3x^2-6x\)
Gọi hoành độ của M là \(x_M\)
Hệ số góc của tiếp tuyến của đồ thị (C) tại M bằng 9 tương đương với:
\(f'(x_M)=3x_M^2-6x_M=9\)
\(\Leftrightarrow x_M=3\) hoặc $x_M=-1$
\(\Rightarrow y_M=-2\) hoặc \(y_M=-6\)
Vậy tiếp điểm có tọa độ (3;-2) hoặc (-1;-6)
Đáp án B
Câu 2:
Gọi hoành độ tiếp điểm là $x_0$
Hệ số góc của tiếp tuyến tại tiếp điểm là:
\(f'(x_0)=x_0^2-4x_0+3\)
Vì tt song song với \(y=3x-\frac{20}{3}\Rightarrow f'(x_0)=3\)
\(\Leftrightarrow x_0^2-4x_0+3=3\Leftrightarrow x_0=0; 4\)
Khi đó: PTTT là:
\(\left[{}\begin{matrix}y=3\left(x-0\right)+f\left(0\right)=3x+4\\y=3\left(x-4\right)+f\left(4\right)=3x-\dfrac{20}{3}\end{matrix}\right.\) (đt 2 loại vì trùng )
Do đó \(y=3x+4\Rightarrow \) đáp án A
Câu 3:
PT hoành độ giao điểm:
\(\frac{2x+1}{x-1}-(-x+m)=0\)
\(\Leftrightarrow x^2+(1-m)x+(m+1)=0\) (1)
Để 2 ĐTHS cắt nhau tại hai điểm pb thì (1) phải có hai nghiệm phân biệt
\(\Leftrightarrow \Delta=(1-m)^2-4(m+1)> 0\)
\(\Leftrightarrow m^2-6m-3> 0\)
\(\Leftrightarrow\left[{}\begin{matrix}m< 3-2\sqrt{3}\\m>3+2\sqrt{3}\end{matrix}\right.\)
Kết hợp với m nguyên và \(m\in (0;10)\Rightarrow m=7;8;9\)
Có 3 giá trị m thỏa mãn.

a) Tập xác định: R; y' = 3(1 - x2); y' = 0 ⇔ x = ± 1 .
Bảng biến thiên :
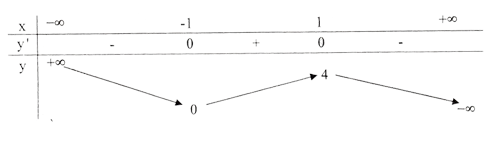
Đồ thị như hình bên.
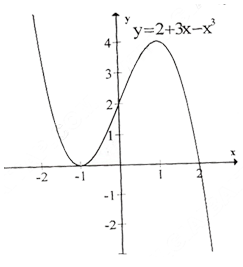
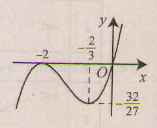
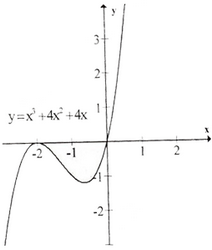
b) Tập xác định : R ; y' = 3x2 + 8x + 4; y' = 0 ⇔ x= -2, x = ![]() .
.
Bảng biến thiên :
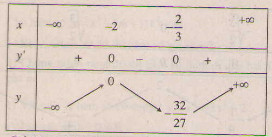
Đồ thị như hình bên.
c) Tập xác định : R ;
y' = 3x2 + 2x + 9 > 0, ∀x. Vậy hàm số luôn đồng biến, không có cực trị.
Bảng biến thiên :
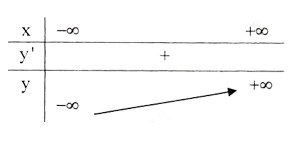
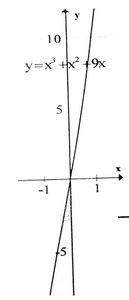
Đồ thị hàm số như hình bên.
d) Tập xác định : R ;
y' = -6x2 ≤ 0, ∀x. Vậy hàm số luôn nghịch biến, không có cực trị.
Bảng biến thiên :
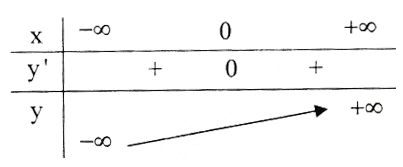
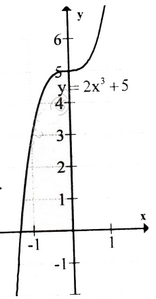
Đồ thị hàm số như hình bên.
Lời giải hay đó!!!
Nhưng không biết người giải nó có hiểu nó không....![]() (thở dài)
(thở dài)

a) Tập xác định : R\ {1}; y′=−4(x−1)2<0,∀x≠1y′=−4(x−1)2<0,∀x≠1 ;
Tiệm cận đứng : x = 1 . Tiệm cận ngang : y = 1.
Bảng biến thiên :
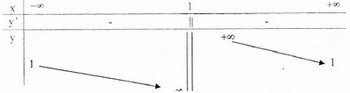
Đồ thị như hình bên. 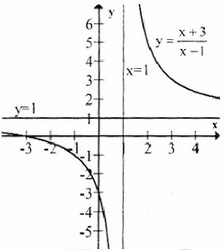
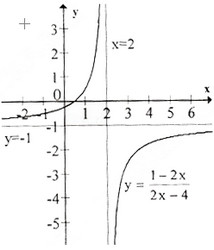
b) Tập xác định : R \{2}; y′=6(2x−4)2>0,∀x≠2y′=6(2x−4)2>0,∀x≠2
Tiệm cận đứng : x = 2 . Tiệm cận ngang : y = -1.
Bảng biến thiên :
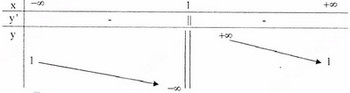
Đồ thị như hình bên.
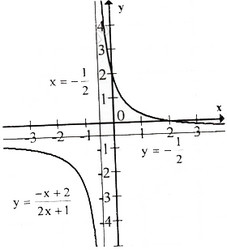
c) Tập xác định : R∖{−12}R∖{−12}; y′=−5(2x+1)2<0,∀x≠−12y′=−5(2x+1)2<0,∀x≠−12
Tiệm cận đứng : x=−12x=−12 . Tiệm cận ngang : y=−12y=−12.
Bảng biến thiên :
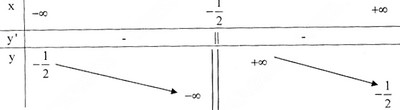
Đồ thị như hình bên.
`a)TXĐ: R`
`b)TXĐ: R\\{0}`
`c)TXĐ: R\\{1}`
`d)TXĐ: (-oo;-1)uu(1;+oo)`
`e)TXĐ: (-oo;-1/2)uu(1/2;+oo)`
`f)TXĐ: (-oo;-\sqrt{2})uu(\sqrt{2};+oo)`
`h)TXĐ: (-oo;0) uu(2;+oo)`
`k)TXĐ: R\\{1/2}`
`l)ĐK: {(x^2-1 > 0),(x-2 > 0),(x-1 ne 0):}`
`<=>{([(x > 1),(x < -1):}),(x > 2),(x ne 1):}`
`<=>x > 2`
`=>TXĐ: (2;+oo)`
câu l) $x^2-1 > 0$ thì giải ra 2 nghiệm $x < -1, x > 1$ mới đúng chứ nhỉ?