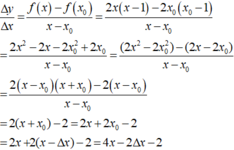AH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
28 tháng 4 2021
\(y=x^3-3x^2+2x+2\Rightarrow y'=3x^2-6x+2\)
Vi \(\Delta\perp d:y=x-3\Rightarrow y'=-1\Leftrightarrow3x^2-6x+2=-1\)
\(\Rightarrow x=1\Rightarrow y=1-3+2+2=2\)
\(\Rightarrow\Delta:y=-1\left(x-1\right)+2\)
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 7 2021
Gọi M là 1 điểm thuộc denta và M' là ảnh của M
\(\left\{{}\begin{matrix}x'=x-4\\y'=y+2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=x'+4\\y=y'-2\end{matrix}\right.\)
Thế vào pt denta:
\(2\left(x'+4\right)-\left(y'-2\right)-5=0\Leftrightarrow2x'-y'+5=0\)
Vậy đường thẳng đó là \(2x-y+5=0\)
CM
6 tháng 12 2019
∆y=f(1+∆x)-f(1)=(1+∆x)2+2(1+∆x)-(1+2)=(∆x)2+4∆x
Đáp án B
Chú ý. Tránh các sai lầm thay trực tiếp ∆x hoặc 1 vào hàm (A,D) hoặc lấy hiệu của f(∆x) và f(1) (C)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 8 2020
1.
\(y=1+cosx.sin\left(\pi+\frac{\pi}{2}-2x\right)=1-cosx.cos2x\)
\(y\left(-x\right)=1-cos\left(-x\right).cos\left(-2x\right)=1-cosx.cos2x=y\left(x\right)\)
Hàm chẵn
2.
\(1+2cosx\ge0\Leftrightarrow cosx\ge-\frac{1}{2}\)
\(\Leftrightarrow-\frac{2\pi}{3}+k2\pi\le x\le\frac{2\pi}{3}+k2\pi\)