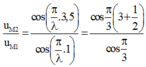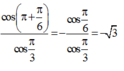Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

\(\lambda = v/f=20/50=0.4cm.\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{4,8-5,3}{0,4}-\frac{0}{2\pi})|=|2a\cos\frac{-5\pi}{4}|=\sqrt{2}a = 2\sqrt{2}\)
\( u_M = A_M\cos(2\pi ft - \pi\frac{d_2+d_1}{\lambda}+\frac{\varphi_1+\varphi_2}{2})=2\sqrt{2}\cos(40 \pi t - \pi\frac{5,3+4,8}{0,4}+\frac{0}{2}) = 2\sqrt{2}\cos(40 \pi t - \pi\frac{5,3+4,8}{0,4})\\ = 2\sqrt{2}\cos(40 \pi t - 25,25\pi)mm.\)

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

a. Theo giả thiết: \(x_1=4\cos(\dfrac{\pi}{6}t_1)=2\sqrt 3\) và $x$ đang giảm, nên ta biểu diễn dao động này bằng véc tơ quay:
> M x 4 30 O N -2
Thời điểm $t_1$, véc tơ quay tại vị trí M.
Sau thời điểm $t_1$ một khoảng $\Delta t = 3s$, véc tơ quay đã quay 1 góc là:
\(\alpha = \omega.t = \dfrac{\pi}{6}.3=\dfrac{\pi}{2}(rad)\)
Lúc này, véc tơ quay đã quay đến N. Từ giản đồ véc tơ ở trên ta suy ra li độ: $x = -2cm$
b. Bước sóng: \(\lambda=v.t=2.12=24cm\)
Điểm M trễ pha hơn O là: \(\Delta \varphi = \dfrac{2\pi.d}{\lambda}=\dfrac{2\pi.40}{24}=\dfrac{10\pi}{3}(rad)\)
Biểu diễn trạng thái dao động của M theo O ở thời điểm $t_1$ trên giản đồ véc tơ, ta có:
O M > x 4
Từ giản đồ trên dễ dàng suy được li độ của M là \(-2\sqrt 3cm\)

Áp dụng công thức: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2=2,5^2+\dfrac{(50\sqrt 3)^2}{\omega^2}=(2,5\sqrt 3)^2+\dfrac{50^2}{\omega^2}\)
\(\Rightarrow \omega = 20(rad/s)\)
Và \(A=5cm\)

Đây em nhé Câu hỏi của Nguyễn Thị Trúc Đào - Vật lý lớp 12 | Học trực tuyến
 chọn A
chọn A
Đáp án D
Hai nguồn giống nhau, có λ = 3 c m nên phương trình sóng tại M 1 và M 2 là:
Mà M 1 và M 2 nằm trên cùng một elip nên ta luôn có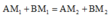
Nên ta có tỉ số