Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc PAO+góc PMO=180 độ
=>PAOM nội tiếp
Xét (O) có
PA,PM là tiếp tuyến
=>PA=PM
mà OA=OM
nên OP là trung trực của AM
=>OP vuông góc AM
góc AMB=1/2*sđ cung AB=90 độ
=>MB vuông góc AM
=>OP//MB
b: Xét ΔPAO vuông tại A và ΔNOB vuông tại O có
OA=OB
góc POA=góc NBO
=>ΔPAO=ΔNOB
=>PO=NB
mà PO//NB
nên POBN là hình bình hành

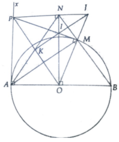
a, HS tự làm
b, Ta có OP ⊥ AM, BM ⊥ AM => BM//OP
c, chứng minh ∆AOP = ∆OBN => OP=BN
lại có BN//OP do đó OPNB là hình bình hành
d, Ta có ON ⊥ PI, PM ⊥ JO mà PM ∩ ON = I => I là trực tâm ∆POJ => JI ⊥ PO(1)
Chứng minh PAON hình chữ nhật => K trung điểm PO
Lại có A P O ^ = O P I ^ = I O P ^ => ∆IPO cân tại I => IKPO (2)
Từ (1),(2) => J,I,K thẳng hàng
Bài 3 :
a, Thay m = -2 ta được
\(x^2-2\left(-1\right)x-2-2=0\Leftrightarrow x^2+2x-4=0\Leftrightarrow\left(x+1\right)^2-5=0\)
\(\Leftrightarrow\left(x+1-\sqrt{5}\right)\left(x+1+\sqrt{5}\right)=0\Leftrightarrow x=-1\pm\sqrt{5}\)
b, Để pt có 2 nghiệm pb \(\Delta'=\left(m+1\right)^2-\left(m-2\right)=m^2+m+3>0\)
Theo Vi et \(\hept{\begin{cases}x_1+x_2=2\left(m+1\right)\\x_1x_2=m-2\end{cases}}\Leftrightarrow\hept{\begin{cases}x_1+x_2=2m+2\\x_1x_2=m-2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=\frac{x_1+x_2-2}{2}\\m=x_1x_2+2\end{cases}}\)
Ta có \(\frac{x_1+x_2-2-2x_1x_2-4}{2}=0\Leftrightarrow x_1+x_2-2x_1x_2-6=0\)
Bài 4 :
a, Vì PA ; PM là tiếp tuyến của đường tròn (O) với A;M là tiếp điểm
=> ^OAP = ^OMP = 900
Xét tứ giác APMO có
^OAP + ^OMP = 1800 mà 2 góc này đối
Vậy tứ giác APMO là tứ giác nt 1 đường tròn
b, Ta có ^AMB = 900 ( góc nt chắn nửa đường tròn )
=> AM vuông MB (1)
Lại có PA = PM ( tc tiếp tuyến cắt nhau )
OA = OM = R
Vậy PO là đường trung trực đoạn AM => PO vuông AM (2)
Từ (1) ; (2) suy ra MB // PO