
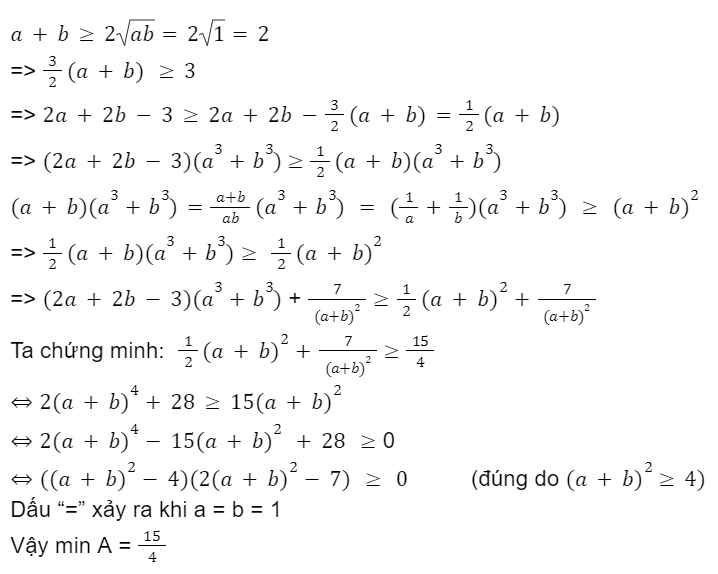
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

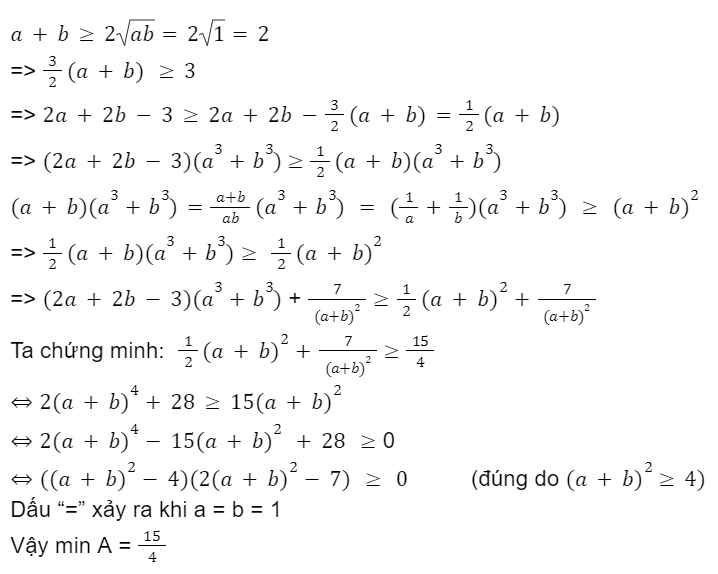

Câu 1:
\(a^3+a^2b-ab^2-b^3\)
\(=a^2\left(a+b\right)-b^2\left(a+b\right)\)
\(=\left(a+b\right)\left(a^2-b^2\right)\)
\(=\left(a+b\right)\left(a-b\right)\left(a+b\right)\)
\(=\left(a+b\right)^2\left(a-b\right)\)
Câu 2:
\(a\left(b^3-c^3\right)+b\left(c^3-a^3\right)+c\left(a^3-b^3\right)\)
\(=a\left(b^3-c^3\right)+bc^3-a^3b+a^3c-b^3c\)
\(=a\left(b-c\right)\left(b^2+bc+c^2\right)-a^3\left(b-c\right)-bc\left(b-c\right)\left(b+c\right)\)
\(=\left(b-c\right)\left(ab^2+abc+c^2a-a^3-b^2c-bc^2\right)\)
\(=\left(b-c\right)\left[a\left(c-a\right)\left(c+a\right)-b^2\left(c-a\right)-bc\left(c-a\right)\right]\)
\(=\left(b-c\right)\left(c-a\right)\left(ca+a^2-b^2-bc\right)\)
\(=\left(b-c\right)\left(c-a\right)\left[\left(a-b\right)\left(a+b\right)+c\left(a-b\right)\right]\)
\(=\left(a-b\right)\left(b-c\right)\left(c-a\right)\left(a+b+c\right)\)




Ta có:
\(\left(1-a^2\right)\left(1-b\right)>0\)
\(\Leftrightarrow1+a^2b>a^2+b>a^3+b^3\left(1\right)\)
(Vì \(0< a,b< 1\))
Tương tự ta có:
\(\hept{\begin{cases}1+b^2c>b^3+c^3\left(2\right)\\a+c^2a>c^3+a^3\left(3\right)\end{cases}}\)
Cộng (1), (2), (3) vế theo vế ta được
\(2\left(a^3+b^3+c^3\right)< 3+a^2b+b^2c+c^2a\)