
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số số thỏa mãn: \(\dfrac{9!}{5!}=3024\) số
(Đây là loại hoán vị lặp)

Không gian mẫu: \(C_{27}^4\)
a. Số cách chọn ra 2 bi đỏ: \(C_9^2.C_{18}^2\)
Xác suất: \(P_1=\dfrac{C_9^2.C_{18}^2}{C_{27}^4}=...\)
b. Số cách chọn ra 4 bi có đúng 1 màu: \(C_8^4+C_9^4+C_{10}^4\)
Số cách chọn ra 4 bi có đúng 2 màu: \(C_{17}^4+C_{18}^4+C_{19}^4-2\left(C_8^4+C_9^4+C_{10}^4\right)\)
Số cách chọn ra 4 bi có đủ 3 màu:
\(C_{27}^4-\left(C_{17}^4+C_{18}^4+C_{19}^4-2\left(C_8^4+C_9^4+C_{10}^4\right)+C_8^4+C_9^4+C_{10}^4\right)\)
Xác suất: \(P_2=\dfrac{C_{27}^4-\left(C_{17}^4+C_{18}^4+C_{19}^4-\left(C_8^4+C_9^4+C_{10}^4\right)\right)}{C_{27}^4}=...\)
c. Xác suất: \(P_3=1-P_2=...\)

Đáp án A
Xác suất để Anh được điểm bằng xác suất Anh trả lời đúng câu trong câu còn lại bằng
![]()

a. Chọn 3 người bất kì từ 100 người, có \(C_{100}^3\) cách
b. Chọn 2 nam từ 60 nam và 1 nữ từ 40 nữ, có \(C_{60}^2.C_{40}^1\) cách
c. Do anh A và chị B không đi nên chỉ chọn 3 người từ 98 người còn lại, có \(C_{98}^3\) cách
d. Chọn anh A và chị B đi chung (nghĩa là chỉ cần chọn 1 người từ 98 người còn lại): \(C_{98}^1\) cách
\(\Rightarrow\) Số cách để anh A và chị B không đi chung là: \(C_{100}^3-C_{98}^1\)
a) Để tính số đoàn đại biểu 3 người có thể thành lập nếu không ai từ chối tham gia, ta sử dụng công thức tổ hợp. Tổng số cách chọn 3 người từ 100 người là:
C3100=100!3!(100−3)!=161700�1003=100!3!(100−3)!=161700b) Để tính số đoàn có thể thành lập nếu có 2 nam và 1 nữ, ta sẽ tính số cách chọn 2 nam từ 60 nam và chọn 1 nữ từ 40 nữ, sau đó nhân kết quả lại với nhau:

Gọi x(đồng) là số tiền mua 1 mớ rau cải (x>0)
y(đồng) là số tiền mua 1 cân thịt lợn (y>0)
Vì chị Hạnh đi chợ mua 3 mớ rau cải và nửa cân thịt lợn hết 95 ngàn nên ta có pt:
\(3x+0,5y=95000\left(1\right)\)
Vì anh Phúc đi chợ mua 5 mớ rau cải và 2 cân thịt lợn hết 345 ngàn nên ta có pt:
\(5x+2y=345000\left(2\right)\)
Từ (1) và (2) ta có hpt \(\left\{{}\begin{matrix}3x+0,5y=95000\\5x+2y=345000\end{matrix}\right.\)
Giải hpt ta được \(\left\{{}\begin{matrix}x=5000\\y=160000\end{matrix}\right.\) (nhận)
Vậy ...

Từ đề bài ta suy ra trong 30 người có đúng 15 cặp hiệp sĩ – kẻ lừa dối là bạn của nhau. Ta có thể dễ dàng đoán được đáp số của bài toán bằng cách “giả định” 15 người ở vị trí lẻ đều là hiệp sĩ. Khi đó, dĩ nhiên bạn của họ đều ngồi cạnh ở các vị trí chẵn và đều là kẻ lừa dối, do đó không có ai nói “Đúng”. Đáp số là 0.
Tuy nhiên, đó chỉ là dự đoán đáp số chứ không phải lời giải. Với cách hỏi ở đề bài, ta biết đáp số là 0. Nhưng để khẳng định điều này, ta phải chứng minh chứ không chỉ là đưa ra một ví dụ như vậy.
Nếu chúng ta sa đà vào việc xét vị trí ngồi của 30 người (ai là hiệp sĩ, ai là kẻ nối dối) thì sẽ rất rối vì có nhiều trường hợp xảy ra. Bí quyết của lời giải là ở nhận xét quan trọng sau: Trong 2 người là bạn của nhau, chỉ có đúng 1 người nói “Đúng” cho câu hỏi "Có phải bạn của anh đang ngồi cạnh anh không?".
Thật vậy, nếu có hai người, 1 hiệp sĩ, 1 kẻ lừa dối là bạn của nhau. Xét 2 trường hợp:
1) Nếu họ ngồi cạnh nhau thì hiệp sĩ sẽ nói đúng, còn kẻ lừa dối nói “Không”.
2) Nếu họ không ngồi cạnh nhau thì hiệp sĩ nói “Không”, còn kẻ lừa dối nói “Đúng”.
Như vậy, vì ta có 15 cặp bạn nên ta có đúng 15 câu trả lời “Đúng”. Vì cả 15 người ở vị trí lẻ đã nói “Đúng” nên tất cả những người ở vị trí chẵn đều nói “Không”. Tức là đáp số bằng 0.
Từ đề bài ta suy ra trong 30 người có đúng 15 cặp Hiệp sĩ – Kẻ lừa dối là bạn của nhau. Ta có thể dễ dàng đoán được đáp số của bài toán bằng cách “giả định” 15 người ở vị trí lẻ đều là Hiệp sĩ. Khi đó, dĩ nhiên bạn của họ đều ngồi cạnh họ ở các vị trí chẵn và đều là Kẻ lừa dối, do đó không có ai nói “Đúng”. Đáp số là 0.
Tuy nhiên, đó chỉ là dự đoán đáp số chứ không phải lời giải. Với cách hỏi ở đề bài, ta biết đáp số là 0. Nhưng để khẳng định điều này, ta phải chứng minh chứ không chỉ là đưa ra một ví dụ như vậy.
Nếu chúng ta sa đà vào việc xét vị trí ngồi của 30 người (ai là hiệp sĩ, ai là kẻ nối dối) thì sẽ rất rối vì có nhiều trường hợp xảy ra. Bí quyết của lời giải là ở nhận xét quan trọng sau: Trong 2 người là bạn của nhau, chỉ có đúng 1 người nói “Đúng” cho câu hỏi "Có phải bạn của anh đang ngồi cạnh anh không?".
Thật vậy, nếu có hai người, 1 hiệp sĩ, 1 kẻ lừa dối là bạn của nhau. Xét 2 trường hợp:
1) Nếu họ ngồi cạnh nhau thì Hiệp sĩ sẽ nói đúng, còn Kẻ lừa dối nói “Không”.
2) Nếu họ không ngồi cạnh nhau thì Hiệp sĩ nói “Không”, còn Kẻ lừa dối nói “Đúng”.
Như vậy, vì ta có 15 cặp bạn nên ta có đúng 15 câu trả lời “Đúng”. Vì cả 15 người ở vị trí lẻ đã nói “Đúng” nên tất cả những người ở vị trí chẵn đều nói “Không”. Tức là đáp số bằng 0.
Chú ý rằng ta không biết được trong 15 người ở vị trí lẻ có bao nhiêu người là Hiệp sĩ, có bao nhiêu người là Kẻ lừa dối và họ xếp ở những vị trí nào.

Chọn D
*) Ta có: ![]()
*) Tính n(A): Giả sử 8 chữ số được viết vào 8 ô trống được đánh số từ 1 đến 8
TH1: Xếp bất kỳ
Xếp hai chữ số 1, hai chữ số 2 và 4 chữ số còn lại: Có ![]() (cách).
(cách).
TH2: Số các cách xếp sao cho không thỏa mãn yêu cầu bài toán
Xếp hai chữ số 1 đứng liền nhau: Có ![]() cách.
cách.
Xếp hai chữ số 2 đứng liền nhau: Có ![]() cách.
cách.
Số các cách xếp thuộc cả hai trường hợp trên:
+ Coi hai chữ số 1đứng liền nhau là nhóm X, hai chữ số 2 đứng liền nhau là nhóm Y
+ Xếp X, Y và 4 số còn lại có: ![]() (cách)
(cách)
Vậy số cách xếp không thỏa mãn yêu cầu là: ![]() (cách)
(cách)
Vậy ![]()
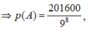

a) \(100+98+96+...+2-97-95-93-...-3\)
= \(100+98+\left(96-97\right)+\left(94-95\right)+...+\left(2-3\right)\)
= \(100+98-95\) = \(103\)
b) \(2-4-6+8+10-12-14+16+...-102+104\)
= \(\left(2-4\right)+\left(-6+8\right)+\left(10-12\right)+\left(-14+16\right)+...+\left(-102+104\right)\)
= \(-2+2-2+2-2+...+2\) = \(0\)
c) \(1+2-3-4+5+6-7-8+9+10-11-12+...-111-112+113+114\)
= \(\left(1+2\right)-\left(3+4\right)+\left(5+6\right)-\left(7+8\right)+...\left(113+114\right)\)
= \(3-7+11-15+19-23+...+219-223+227\)
= \(\left(3-7\right)+\left(11-15\right)+\left(19-23\right)+...+\left(219-223\right)+227\)
= \(-4-4-4-4-...-4+227\)
= \(54\left(-4\right)+227\) = \(-216+227\) = \(11\)
các anh chị chẳng nhường nhịn em nó j cả mới lớp 1 thôi sao cứ chửi nó =))))
OK lớp 1