IE
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 7 2017
Đề là j, chứng minh hay tìm n để thỏa mãn ddieuf kiện j đó hả b
17 tháng 4 2018
\(M=\frac{9}{49}-\frac{11}{60}+\frac{13}{84}-\frac{15}{112}\)
\(M=\frac{1}{2940}+\frac{1}{48}\)
\(M=\frac{83}{3920}\)
PT
4
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
31 tháng 8
- 5\(x\) - 178 = 14\(x\) + 145
14\(x\) + 5\(x\) = - 178 - 145
19\(x\) = - 323
\(x\) = - 323 : 19
\(x\) = - 17
Vậy \(x=-17\)
31 tháng 8
\(-5x-178=14x+145\)
\(\Rightarrow14x+5x=-178-145\)
\(\Rightarrow19x=-178-145\)
\(\Rightarrow19x=-323\)
\(\Rightarrow x=-323:19\)
\(\Rightarrow x=-17\)
Vậy \(x=-17\)
DD
3
13 tháng 3 2022
\(3n-2\inƯ\left(15\right)\) \(=\left\{1;-1;3;-3;5;-5;15;-15\right\}.\)
\(\Leftrightarrow n\in\left\{1;\dfrac{1}{3};\dfrac{5}{3};\dfrac{-1}{3};\dfrac{7}{3};-1;\dfrac{17}{3};\dfrac{-13}{3}\right\}.\)
Mà \(n\ne\dfrac{2}{3};n\in Z.\)
\(\Rightarrow n\in\left\{1;-1\right\}.\)
10 tháng 10 2018
781 . 152018
781\(\equiv\)( mod 10 )
710\(\equiv\)9 ( mod 10 )
780\(\equiv\)1 ( mod 10 )
781\(\equiv\)7 ( mod 10 )
Vậy chữ số tận cùng của 781 là 1
152018\(\equiv\)( mod 10 )
158\(\equiv\)5 ( mod 10 )
1580\(\equiv\)5 ( mod 10 )
15960\(\equiv\)5 ( mod 10 )
151920\(\equiv\)5 ( mod 10 )
152000\(\equiv\)5 ( mod 10 )
152007\(\equiv\)5 ( mod 10 )
152014\(\equiv\)5 ( mod 10 )
152018\(\equiv\)5 ( mod 10 )
Vậy chữ số tận cùng của 152018 là 5
\(\Rightarrow\)Chữ số tận cùng của 781 . 152018 là 7 . 5 = 35
Vậy chữ số tận cùng của 781 . 152018 là 5
Hk tốt
NM
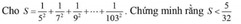
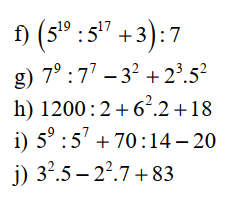giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim
1
13 tháng 12 2021
\(f,=\left(5^2+3\right):7=28:7=4\\ g,=7^2-9+8\cdot25=49-9+200=240\\ h,=600+72+18=690\\ i,=5^2+5-20=10\\ j,=45-28+83=100\)
=1095656855851