Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B/A
\(=\dfrac{1+\dfrac{2020}{2}+1+\dfrac{2019}{3}+...+1+\dfrac{1}{2021}+1}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}}\)
\(=\dfrac{2022\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}}=2022\)

Ta có : A = \(\frac{10^{2020}+1}{10^{2021}+1}\)
=> 10A = \(\frac{10^{2021}+10}{10^{2021}+1}=1+\frac{9}{10^{2021}+1}\)
Lại có : \(B=\frac{10^{2021}+1}{10^{2022}+1}\)
=> \(10B=\frac{10^{2022}+10}{10^{2022}+1}=1+\frac{9}{10^{2022}+1}\)
Vì \(\frac{9}{10^{2022}+1}< \frac{9}{10^{2021}+1}\)
=> \(1+\frac{9}{10^{2022}+1}< 1+\frac{9}{10^{2022}+1}\)
=> 10B < 10A
=> B < A
b) Ta có : \(\frac{2019}{2020+2021}< \frac{2019}{2020}\)
Lại có : \(\frac{2020}{2020+2021}< \frac{2020}{2021}\)
=> \(\frac{2019}{2020+2021}+\frac{2020}{2020+2021}< \frac{2019}{2020}+\frac{2020}{2021}\)
=> \(\frac{2019+2020}{2020+2021}< \frac{2019}{2020}+\frac{2020}{2021}\)
=> B < A

\(B=\left(\dfrac{2020}{2}+1\right)+\left(\dfrac{2019}{3}+1\right)+...+\left(\dfrac{1}{2021}+1\right)+1\)
\(=\dfrac{2022}{2}+\dfrac{2022}{3}+...+\dfrac{2022}{2021}+\dfrac{2022}{2022}\)
=2022(1/2+1/3+...+1/2021+1/2022)
=>B/A=2022

bài 1:
ssh của A là:
(151-3):2+1=75
A=(151+3)x75:2=5775
đáp số: 5775
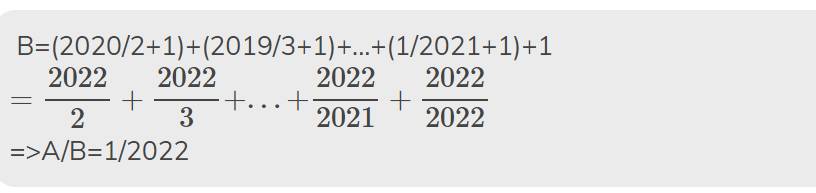

Ta có:
\(\frac{2021}{1}+\frac{2020}{2}+\frac{2019}{3}+...+\frac{2}{2020}+\frac{1}{2021}\)
\(=1+\frac{2020}{2}+1+\frac{2019}{3}+...+1+\frac{2}{2020}+1+\frac{1}{2021}+1\)
\(=\frac{2022}{2}+\frac{2022}{3}+...+\frac{2022}{2020}+\frac{2022}{2021}+\frac{2022}{2022}\)
\(=2022\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2020}+\frac{1}{2021}+\frac{1}{2022}\right)\)
Do đó giá trị của \(M\)là:
\(M=\frac{2022\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2020}+\frac{1}{2021}+\frac{1}{2022}\right)}{\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2020}+\frac{1}{2021}+\frac{1}{2022}}=2022\)
2021/1 + 2/2020 + 2019/3 + ... + 2/2020 + 1/2021
M = _______________________________________
1/2 + 1/3 + ... + 1/2020 + 1/2021 + 1/2022
=\(\frac{2022+\frac{2022}{2}+...+\frac{2022}{2021}-2021}{\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2022}}=\frac{1+\frac{2022}{2}+...+\frac{2022}{2021}}{\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2022}}\)
=2022