Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C
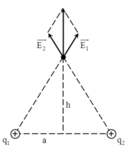
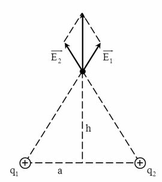
Cường độ điện trường tại điểm M là
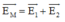
Trong đó E 1 → , E 2 → là cường độ điện trường do q 1 và q 2 gây ra tại M:
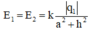
Suy ra: Cường độ điện trường tổng hợp tại M:
E M = 2 E 1 cos α = 2 k q h a 2 + h 2 1,5 V / m
Áp dụng bất đẳng thức Cô-si, ta có:
a 2 + h 2 = a 2 2 + a 2 2 + h 2 ≥ 3 a 4 h 2 4 3 ⇒ a 2 + h 2 3 ≥ 27 4 a 4 h 2
⇒ a 2 + h 2 3 2 ≥ 3 3 2 a 2 h
Vậy E M ≤ 2 k q h 3 3 2 a 2 h = 4 k q 3 3 a 2
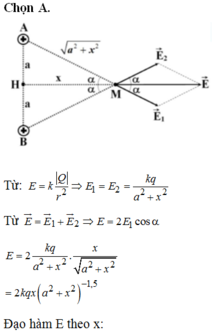
EM cực đại khi h = a 2 ⇒ E M max = 4 k q 3 3 a 2
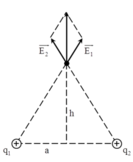
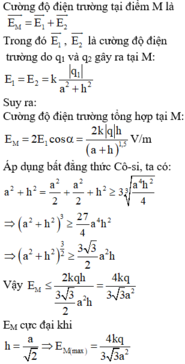
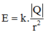
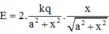
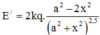

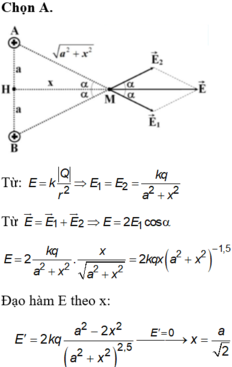
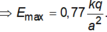
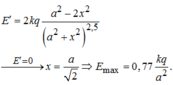
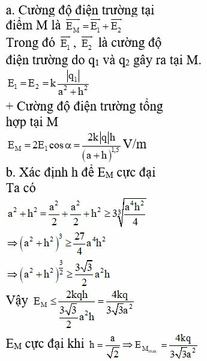
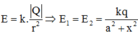
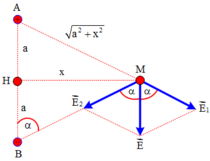
Gọi H là trung điểm AB. Ta có:
\(E_A=E_B=\frac{kq}{AM^2}=\frac{kq}{\sqrt{a^2+h^2}}\)
\(E_M=\sqrt{E_A^2+E_B^2+2E_AE_B.cos\left(AMB\right)}\)
\(=\sqrt{2E_A^2+2E_A^2.\left(2cos^2\alpha-1\right)}\)
\(=\sqrt{4E_A^2.cos^2\alpha}=2E_A.cos\alpha\)
\(=\frac{2kq}{a\sqrt{a^2+h^2}}\)
Dễ thấy\(E_M\) đạt gtln khi \(h=0\Leftrightarrow E_M=\frac{2kq}{a^2}\)