Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x O y n m a o 80 o
a, Hai góc \(\widehat{xOm}\) và \(\widehat{yOm}\)kề bù nên \(\widehat{xOm}=180^0-\widehat{yOm}=180^0-80^0=110^0\)
Hai tia On,Om cùng thuộc một nửa mặt phẳng bờ chứa tia Ox mà \(\widehat{xOn}< \widehat{xOm}\) nên tia On nằm giữa hai tia Ox,Om
Hai góc xOn và yOn kề bù nên \(\widehat{xOn}+\widehat{yOn}=180^0\)mà \(\widehat{xOn}< 100^0\)nên \(\widehat{yOn}>80^0\). Hai tia Om,On cùng thuộc một nửa mặt phẳng bờ chứa tia Oy mà \(\widehat{yOm}< \widehat{yOn}\)nên tia Om nằm giữa hai tia Oy và On
b, Ta có : \(\widehat{mOn}=180^0-(80^0+a^0)=100^0-a^0\)để cho \(\widehat{mOn}=\frac{\widehat{xOn}+\widehat{yOm}}{2}\)thì phải có :
\(\frac{a^0+80^0}{2}=100^0-a^0\)
\(a^0+80^0=2(100^0-a^0)\)
\(a^0+80^0=200^0-2a^0\)
\(3a^0=120^0\)
\(a^0=120^0:3=40^0\)
Vậy : ....

Bài 2:
a)
Sửa đề: Tính \(\widehat{yOz}\)
Ta có: \(\widehat{xOy}+\widehat{yOz}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{yOz}+110^0=180^0\)
hay \(\widehat{yOz}=70^0\)
b) Ta có: Om là tia phân giác của \(\widehat{xOy}\)
nên \(\widehat{xOm}=\dfrac{\widehat{xOy}}{2}=\dfrac{110^0}{2}=55^0\)
Ta có: \(\widehat{xOm}+\widehat{mOz}=180^0\)(hai góc kề bù)
nên \(\widehat{mOz}=180^0-\widehat{xOm}=180^0-55^0=125^0\)
Ta có: On là tia phân giác của \(\widehat{yOz}\)
nên \(\widehat{zOn}=\dfrac{\widehat{zOy}}{2}=\dfrac{70^0}{2}=35^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia Oz, ta có: \(\widehat{zOn}< \widehat{zOm}\left(35^0< 125^0\right)\)
nên tia On nằm giữa hai tia Oz và Om
\(\Leftrightarrow\widehat{zOn}+\widehat{mOn}=\widehat{zOm}\)
\(\Leftrightarrow35^0+\widehat{mOn}=125^0\)
hay \(\widehat{mOn}=90^0\)
Vậy: \(\widehat{mOn}=90^0\)

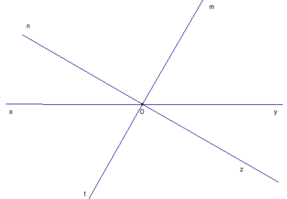
a, Do xy là đuờng thẳng
=> \(\widehat{xOy}\)=\(180^0\)(1)
Mà \(\widehat{xOM}\)=\(^{60^o}\)(2)
Từ (1) và (2):
=>\(\widehat{MOy}\)= \(\widehat{xOy}\)-\(\widehat{MOx}\)
= \(180^0\)-\(60^0\)=\(120^0\)
Vậy \(\widehat{MOy}\)=\(120^0\)
b, Do \(\widehat{xON}\)phụ với \(\widehat{xOM}\)
=>\(\widehat{xON}\)+\(\widehat{MON}\)=\(90^0\)
=>\(60^0\)+\(\widehat{MON}\)=\(90^0\)
=>\(\widehat{MON}\)=\(30^0\)
Vậy \(\widehat{MON}\)=\(30^0\)
k cho mình nha...cảm ơn bạn
x y O M N 60
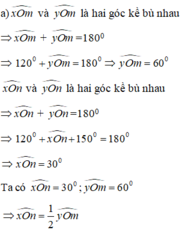



Hình:
x O y m n 150 50
Giải:
+ Ta có: \(\widehat{yOn}< \widehat{xOy}\left(50^0< 180^0\right)\)
Ta có đẳng thức:
\(\widehat{yOn}+\widehat{xOn}=\widehat{xOy}\)
Hay \(50^0+\widehat{xOn}=180^0\)
\(\Leftrightarrow\widehat{xOn}=180^0-50^0=130^0\)
+ Ta có: \(\widehat{xOm}< \widehat{xOy}\left(150^0< 180^0\right)\)
Ta có đẳng thức:
\(\widehat{xOm}+\widehat{yOm}=\widehat{xOy}\)
Hay \(150^0+\widehat{yOm}=180^0\)
\(\Leftrightarrow\widehat{yOm}=180^0-150^0=30^0\)
+ Ta có: \(\widehat{yOm}< \widehat{yOn}\left(30^0< 50^0\right)\)
Ta có đẳng thức:
\(\widehat{yOm}+\widehat{mOn}=\widehat{yOn}\)
Hay \(30^0+\widehat{mOn}=50^0\)
\(\Leftrightarrow\widehat{mOn}=50^0-30^0=20^0\)
Vậy ...