BT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2023
Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow xyz=1\) và \(x;y;z>0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P=\dfrac{1}{\dfrac{1}{x^3}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)}+\dfrac{1}{\dfrac{1}{y^3}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)}+\dfrac{1}{\dfrac{1}{z^3}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(=\dfrac{x^3yz}{y+z}+\dfrac{y^3zx}{z+x}+\dfrac{z^3xy}{x+y}=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
\(P\ge\dfrac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
22 tháng 3
Đặt \(a = \frac{1}{x} ; b = \frac{1}{y} ; c = \frac{1}{z} \Rightarrow x y z = 1\) và \(x ; y ; z > 0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P = \frac{1}{\frac{1}{x^{3}} \left(\right. \frac{1}{y} + \frac{1}{z} \left.\right)} + \frac{1}{\frac{1}{y^{3}} \left(\right. \frac{1}{z} + \frac{1}{x} \left.\right)} + \frac{1}{\frac{1}{z^{3}} \left(\right. \frac{1}{x} + \frac{1}{y} \left.\right)}\)
\(= \frac{x^{3} y z}{y + z} + \frac{y^{3} z x}{z + x} + \frac{z^{3} x y}{x + y} = \frac{x^{2}}{y + z} + \frac{y^{2}}{z + x} + \frac{z^{2}}{x + y}\)
\(P \geq \frac{\left(\left(\right. x + y + z \left.\right)\right)^{2}}{y + z + z + x + x + y} = \frac{x + y + z}{2} \geq \frac{3 \sqrt[3]{x y z}}{2} = \frac{3}{2}\)
\(P_{m i n} = \frac{3}{2}\) khi \(x = y = z = 1\) hay \(a = b = c = 1\)
QT
.png)
1
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
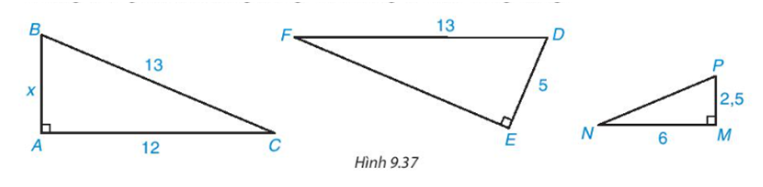
\({x^2} = {4^2} + {2^2} = 20 \Rightarrow x = 2\sqrt 5 \)
\({y^2} = {5^2} - {4^2} = 9 \Leftrightarrow y = 3\)
\({z^2} = {\left( {\sqrt 5 } \right)^2} + {\left( {2\sqrt 5 } \right)^2} = 25 \Rightarrow z = 5\)
\({t^2} = {1^2} + {2^2} = 5 \Rightarrow t = \sqrt 5 \)
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
Những tam giác đồng dạng là
- Tam giác ABC đồng dạng với tam giác EDF với tỉ số đồng dạng là 1
- Tam giác MPN đồng dạng với tam giác ABC với tỉ số đồng dạng là \(\frac{1}{2}\)
- Tam giác MPN đồng dạng với tam giác EDF với tỉ số đồng dạng là \(\frac{1}{2}\)
TC
2
19 tháng 12 2023
Ta có
\(BC\perp AB';B'C'\perp AB'\) => BC//B'C'
\(\Rightarrow\dfrac{AB}{AB'}=\dfrac{BC}{B'C'}\Rightarrow\dfrac{x}{x+h}=\dfrac{a}{a'}\)
\(\Rightarrow a'x=ax+ah\Rightarrow x\left(a'-a\right)=ah\Rightarrow x=\dfrac{ah}{a'-a}\left(dpcm\right)\)
30 tháng 9 2024
Xét tam giác ABCABC có BC⊥ AB′BC⊥ AB′ và B′C′⊥AB′B′C′⊥AB′ nên suy ra BCBC // B′C′B′C′.
Theo hệ quả định lí Thalès, ta có: ABAB′ =BCBC′AB′AB =BC′BC
Suy ra xx+h =aa′x+hx =a′a
a′.x=a(x+h)a′.x=a(x+h)
a′.x−ax=aha′.x−ax=ah
x(a′−a)=ahx(a′−
S
subjects
CTVHS
31 tháng 8
theo đề ta có: \(x+y+z=0\Rightarrow\left(x+y+z\right)^2=0\)
\(\Rightarrow x^2+y^2+z^2+2\cdot\left(xy+yz+zx\right)=0\)
\(\Rightarrow x^2+y^2+z^2=-2\left(xy+yz+xz\right)\left(1\right)\)
ta co: \(x^3+y^3+z^3-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)
mà x + y + z = 0
\(\Rightarrow x^3+y^3+z^3-3xyz=0\Rightarrow x^3+y^3+z^3=3xyz\left(2\right)\)
a. VT = \(\left(x^2+y^2+z^2\right)^2=x^4+y^4+z^4+2\cdot\left(x^2y^2+y^2z^2+x^2z^2\right)\)
ta có: \(\left(xy+yz+zx\right)^2=\left(x^2y^2+y^2z^2+x^2z^2\right)+2xyz\cdot\left(x+y+z\right)\)
vì x+y+z=0 nên: \(\left(xy+yz+zx\right)^2=\left(x^2y^2+y^2z^2+x^2z^2\right)\)
từ (1) ta có: \(\left(x^2+y^2+z^2\right)^2=\left\lbrack-2\left(xy+yz+zx\right)^{}\right\rbrack^2\) (*)
\(=4\cdot\left(xy+yz+zx\right)^2=4\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)\)
ta có: \(4\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)=x^4+y^4+z^4+2\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)\)
mà: \(2\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)=x^4+y^4+z^4\)
thay vào (*) ta được:
\(\left(x^2+y^2+z^2\right)^2=\left(x^4+y^4+z^4\right)+2\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)\)
\(=x^4+y^4+z^4+x^4+y^4+z^4=2\cdot\left(x^4+y^4+z^4\right)=VP\)
⇒ đpcm
b. \(VT=5\cdot\left(x^3+y^3+z^3\right)\left(x^2+y^2+z^2\right)\)
\(=5\cdot\left(3xyz\right)\left(x^2+y^2+z^2\right)\)
\(=15xyz\cdot\left(x^2+y^2+z^2\right)\) (3)
\(x+y+z=0\Rightarrow x+y=-z\)
\(x^5+y^5+z^5=x^5+y^5+\left\lbrack-\left(x+y\right)\right\rbrack^5=x^5+y^5-\left(x+y\right)^5\)
\(=x^5+y^5-\left(x^5+5y^4+10x^3y^2+10x^2y^3+5xy^4+y^5\right)\)
\(=-5x^4y-10x^3y^2-10x^2y^3-5xy^4\)
\(=-5xy\left(x^3+2x^2y+2xy^2+y^3\right)\)
\(=-5xy\left\lbrack x^3+y^3+2xy\left(x+y\right)\right\rbrack\)
\(=-5xy\left\lbrack\left(x+y\right)^3-3xy\left(x+Y\right)+2xy\left(x+y\right)\right\rbrack\)
\(=-5xy\left\lbrack\left(x+Y\right)^3-xy\left(x+y\right)\right\rbrack\)
\(=-5xy\left(x+Y\right)\left\lbrack\left(x+y\right)^2-xy\right\rbrack\)
vì x+y=-z nên ta có:
\(x^5+y^5+z^5=-5xy\left(-z\right)\left\lbrack\left(-z\right)^2-xy\right\rbrack=5xyz\left(x^2-zy\right)\)
mặt khác \(x+y=-z\Rightarrow\left(x+y\right)^2=z^2\Rightarrow x^2+y^2+2xy=z^2\)
\(x^2+y^2+z^2=x^2+y^2+\left(x+y\right)^2\)
\(=x^2+y^2+x^2+2xy+y^2=2\cdot\left(x^2+xy+y^2\right)\)
\(z^2-xy=\left(x+y\right)^2-xy=x^2+2xy+y^2-xy=x^2+xy+y^2\)
vậy \(x^5+y^5+z^5=5xyz\cdot\left(x^2+xy+y^2\right)=\frac52xyz\left(x^2+y^2+z^2\right)\)
\(\Rightarrow2\cdot\left(x^5+y^5+z^5\right)=5xyz\left(x^2+y^2+z^2\right)\)
⇒ \(6\cdot\left(x^5+y^5+z^5\right)=15xyz\left(x^2+y^2+z^2\right)\) (4)
từ (3) và (4) ⇒ VT = VP
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 1 2024
a.
\(A=\left(\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}+\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-2\right)}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+x+1}{x}+\dfrac{x+2}{x}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+3x+1}{x}\right).\dfrac{x}{x+1}\)
\(=\dfrac{x^2+3x+1}{x+1}\)
2.
\(x^3-4x^3+3x=0\Leftrightarrow x\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=1\left(loại\right)\\x=3\end{matrix}\right.\)
Với \(x=3\Rightarrow A=\dfrac{3^2+3.3+1}{3+1}=\dfrac{19}{4}\)
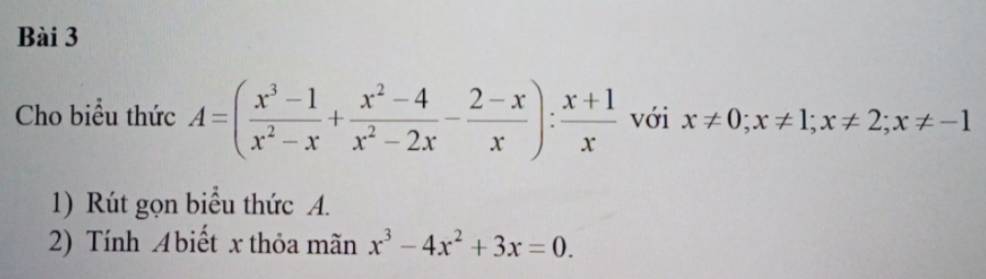
Câu b sai kết quả
Kết quả = 1/x nhé
Câu c sai dòng cuối, dòng cuối vầy nè:
= 2(x - 1)/[(x - 1)(x + 1)]
= 2/(x + 1)
Sao câu c sai dòng cuối v ạ e chưa hiểu ạ