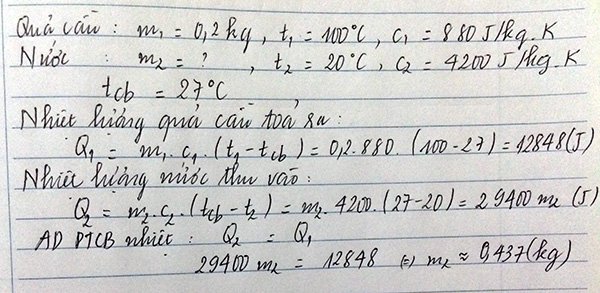Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Nhiệt độ của miếng nhôm ngay khi có cân bằng nhiệt là 27oC.
b) Nhiệt lượng do quả cầu tỏa ra
Q1 = m1C1(t1 –t) = 0,2.880.(100 – 27) = 12848J
c) Nhiệt lượng do nước thu vào để tăng nhiệt độ đến 27oC
Q2 = m2C2(t-t2) = m2.4200.(27-20) = \(29400.m_2\)
Áp dụng phương trình cân bằng nhiệt, ta có:
Q1 = Q2 => 12848= \(29400.m_2\)
m2 =\(\frac{12848}{29400}=0,44kg\)
Vậy khối lượng của nước là 0,44kg.

a) nhiệt lượng tỏa ra của 100 g hơi nước ở 100 độ C giảm xuống còn 10 độ C :
Q1=m1.L +m1.c1.Δ =0,1.2300000+0,1.4200.(100-10)
Q1=267800(J)
nhiệt lượng thu vào của m nước đá ở -4 độ C tăng tới 10 độ C là:
Q2=m.c.Δ+ m.r + m.c.Δ = m.2100.(0-(-4))+m.340000+m.4200.(10-0)
Q2=390400m
PTCBN:
Q1 = Q2
↔267800 = 390400m
↔m=267800/390400
→m gần bằng 0,69 kg

600g=0,6kg
ta có phương trình cân bằng nhiệt:
Qtỏa=Qthu
\(\Leftrightarrow m_1C_1\left(t_1-t\right)=m_2C_2\left(t-t_2\right)\)
\(\Leftrightarrow228\left(100-30\right)=10500\left(30-t_2\right)\)
\(\Rightarrow t_2=28,48\)

4) m nước: 738g
c nước: 4186J/kg.k
m nhiệt lượng kế đồng: 100g
Δt: 17 - 15 = 2
m miếng đồng: 200g
Δt: 100 - 17 = 83
Gọi c của đồng là x, ta có:
Q tỏa = Q thu
738.4186.2 + 100.x.2 = 200.x.83
6178536 + 200x = 16600x
6178536 = 16400x
x = 376.74
Vậy c của đồng là 376.74J/kg.k
6) -Gọi c là nhiệt dung riêng của nước; m là khối lượng nước trong 1 ca
- n1 và n2 lần lượt là số ca nước múc ở thùng A và B
- (n1+n2) là số ca nước có sẵn trong thùng C
-Nhiệt lượng do n1 ca nước ở thùng A đổ vào thùng C đã hấp thụ là: Q1=n1.m.c(50-20)=30cmn1
-Nhiệt lượng do n2 ca nước ở thùng B đổ vào thùng C đã tỏa ra là: Q2=n2.m.c(80-50)=30cmn2
-Nhiệt lượng do (n1+n2) ca nước ở thùng C đã hấp thụ là: Q3=(n1+n2).m.c.(50-40)=10cm(n1+n2)
-Áp dụng PTCB nhiệt; Q1+Q3=Q2
=> 30cmn1+10cm(n1+n2)=30cmn2=>2n1=n2
Vậy khi múc n ca nước ở thùng A phải múc n ca nước ở thùng B và múc 3n ca nước ở thùng C

Cho biết:
\(m_1=0,2kg\)
\(t_1=100^oC\)
\(t_1'=25^oC\)
\(t_2=30^oC\)
\(C_1=380J\)/kg.K
\(C_2=4200J\)/kg.K
Tìm:a) \(t_2=?\)
b) \(Q_1=?\)
c) \(m_2=?\)
Giải:
a) Sau khi thả quả cầu bằng đồng ở \(100^oC\)vào nước ở \(25^oC\) thì nhiệt độ cuối cùng của hệ là \(30^oC\) và đó cũng là nhiệt độ của quả cầu sau khi cân bằng.
b) Nhiệt lượng của quả cầu đồng tỏa ra:
\(Q_1=m_1C_1\left(t_1-t_2\right)\)
\(Q_1=0,2.380\left(100-30\right)\)
\(Q_1=5320\left(J\right)\)
c) Áp dụng phương trình cân bằng nhiệt, ta có:
\(Q_1=Q_2\)
Hay: \(5320=m_2C_2\left(t_2-t_1'\right)\)
\(5320=m_2.4200\left(30-25\right)\)
\(5320=21000m_2\)
\(m_2=0,253\left(kg\right)\)
Đáp số: a) \(t_2=30^oC\)
b) \(Q_1=5320J\)
c) \(m_2=0,253kg\)

gọi:
t là nhiệt độ cân bằng sau khi rót từ bình 1 sang 2
t' là nhiệt độ cân bằng sau khi rót từ bình 2 sang 1
m là khối lượng nước rót
ta có:
rót lần đầu từ bình 1 sang bình 2 thì phương trình cân bằng nhiệt là:
Qtỏa=Qthu
\(\Leftrightarrow mC\left(t_1-t\right)=m_2C\left(t-t_2\right)\)
\(\Leftrightarrow m\left(40-t\right)=2\left(t-20\right)\)
\(\Leftrightarrow40m-mt=2t-40\)
\(\Leftrightarrow2t+mt=40m+40\)
\(\Leftrightarrow t=\frac{40\left(m+1\right)}{2+m}\left(1\right)\)
rót tiếp tục từ bình 2 sang bình 1 thì phương trình cân bằng nhiệt là:
Qtỏa=Qthu
\(\Leftrightarrow\left(m_1-m\right)C\left(t_1-t'\right)=mC\left(t'-t\right)\)
\(\Leftrightarrow\left(4-m\right)\left(40-36\right)=m\left(36-t\right)\)
thế (1) vào phương trình trên ta có:
\(4\left(4-m\right)=m\left(36-\frac{40\left(m+1\right)}{m+2}\right)\)
\(\Leftrightarrow4\left(4-m\right)=m\left(\frac{36\left(m+2\right)-40\left(m+1\right)}{m+2}\right)\)
\(\Leftrightarrow4\left(4-m\right)=m\left(\frac{36m+72-40m-40}{m+2}\right)\)
\(\Leftrightarrow4\left(4-m\right)=\frac{m\left(-4m+32\right)}{m+2}\)
\(\Leftrightarrow\left(16-4m\right)\left(m+2\right)=-4m^2+32m\)
\(\Leftrightarrow16m+32-4m^2-8m+4m^2-32m=0\)
\(\Leftrightarrow-24m+32=0\Rightarrow m=\frac{4}{3}kg\)