Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử phân số và nghịch đảo của nó là: \(\frac{a}{b}\); \(\frac{b}{a}\)
Do phân số dương nên a;b cùng dấu hay a.b > 0
Ta có: \(\frac{a}{b}\)+ \(\frac{b}{a}\)- 2 =\(\frac{a^2+b^2-2ab}{ab}\)= \(\frac{\left(a-b\right)^2}{ab}\)> hoặc = 0
Do đó \(\frac{a}{b}\)+ \(\frac{b}{a}\) > hoặc = 2
Vậy Tổng của 1 phân sô với số nghịch đảo của nó thì không nhỏ hơn 2

Gọi phân số lớn nhất cần tìm là a/b
Ta có:
Theo đề bài thì 8b/15a là số nguyên nên 8b ⋮ 15a
Mà UCLN(8; 15) = 1 và UCLN(a; b) = 1 nên 8 ⋮ a và b ⋮ 15 (1)
Ta lại có :
Tương tự 18b ⋮ 35a
Mà UCLN(18: 35) = 1 và UCLN(a , b) = 1 nên 18⋮ a và b ⋮ 35 (2)
Từ (1), (2) suy ra : a ∈ UC(8; 18) = {0,1,2}
b ∈ UC(15; 35) = {0,105; 210; …}
Vì a/b lớn nhất nên a lớn nhất, b nhỏ nhất khác 0
Vậy phân số cần tìm là 2/105
Gọi phân số lớn nhất cần tìm là a/b
Ta có:
Theo đề bài thì 8b/15a là số nguyên nên 8b ⋮ 15a
Mà UCLN(8; 15) = 1 và UCLN(a; b) = 1 nên 8 ⋮ a và b ⋮ 15 (1)
Ta lại có :
Tương tự 18b ⋮ 35a
Mà UCLN(18: 35) = 1 và UCLN(a , b) = 1 nên 18⋮ a và b ⋮ 35 (2)
Từ (1), (2) suy ra : a ∈ UC(8; 18) = {0,1,2}
b ∈ UC(15; 35) = {0,105; 210; …}
Vì a/b lớn nhất nên a lớn nhất, b nhỏ nhất khác 0
Vậy phân số cần tìm là 2/105

Từng bài 1 thôi bn!
b2: \(\frac{a}{b}\cdot\frac{c}{d}=\frac{2}{5}\left(1\right)\Rightarrow\frac{ac}{bd}=\frac{2}{5}\left(3\right)\)
\(\frac{a}{b}\cdot\left(\frac{c}{d}+3\right)\left(2\right)\Rightarrow\frac{ac}{bd}+\frac{3a}{b}=\frac{28}{15}\left(4\right)\)
(4) thành \(\frac{2}{5}+\frac{3a}{b}=\frac{28}{15}\Rightarrow\frac{a}{b}=\frac{22}{45}\)
(1) thành \(\frac{22}{45}\cdot\frac{c}{d}=\frac{2}{5}\Rightarrow\frac{c}{d}=\frac{9}{11}\)

Gọi hai số cần tìm là a và b.
Suy ra : a = 258 – 126 = 132

b1
tổng số nghịch đảo của hai phân số đó là1/12
b2
thừa số thứ nhất là 22/45
thừa số thứ hai là 9/11
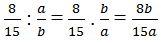
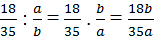
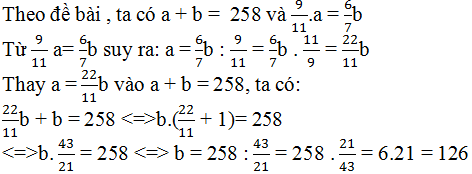
Bài 4:
Gọi hai số cần tìm là a,b
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=258\\\dfrac{9}{11}a-\dfrac{6}{7}b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=132\\b=126\end{matrix}\right.\)