Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có tích 4 số tự nhiên liên tiếp cần tìm là 93024
Vì 93024 ko có chữ số tận cùng là 0 hoặc 5
Suy ra ko có số nào trong đó chứa chữ số tận cùng là 0 hoặc 5
Ta có: 10.10.10.10=10000 (10000<93024)
Suy ra mỗi số tự nhiên liên tiếp trong đó lớn hơn 10 mà 20.20.20.20=160000 (160000>93024)
Suy ra các số tự nhiên liên tiếp nhỏ hơn 20
Mà trong 4 số tự nhiên liên tiếp không có số nào có chữ số tận cùng bằng 0 hoặc 5
Suy ra:
1.Các số tự nhiên liên tiếp đó là:11,12,13,14
11.12.13.14=1716 (loại vì 1716<93024)
2.Các số tự nhiên liên tiếp là:16,17,18,19
16.17.18.19=93024 (chọn )

Đặt tích 2 số tự nhiên liên tiếp là \(a\left(a+1\right)=a^2+a\)
Ta sẽ xét xem tích 2 số tự nhiên liên tiếp chia cho 3 dư bao nhiêu.
TH1: a chia hết cho 3
\(\Rightarrow\)a2 chia hết cho 3 và a cũng chia hết cho 3
\(\Rightarrow a^2+a\) chia hết cho 3
\(\Rightarrow a\left(a+1\right)\) chia hết cho 3
TH2: a chia 3 dư 1 -> a có dạng 3k+1
\(\Rightarrow a^2=\left(3k+1\right)^2=\left(3k+1\right)\left(3k+1\right)=\left(3k+1\right)3k+\left(3k+1\right).1=9k^2+3k+3k+1\)\(=3.\left(3k^2+k+k\right)+1\)
\(\Rightarrow a^2+a=3.\left(3k^2+k+k\right)+1+3k+1=3.\left(3k^2+k+k+k\right)+1+1=3.\left(3k^2+3k\right)+2\)
Thấy \(3.\left(3k^2+3k\right)+2\) chia 3 dư 2
\(\Rightarrow a^2+a\) chia 3 dư 2
\(\Rightarrow a\left(a+1\right)\) chia 3 dư 2
TH3: a chia 3 dư 2
\(\Rightarrow a^2=\left(3k+2\right)^2=\left(3k+2\right)\left(3k+2\right)=\left(3k+2\right).3k+\left(3k+2\right).2=9k^2+6k+6k+4\) \(=3.\left(3k^2+2k+2k\right)+4\)
\(\Rightarrow a^2+a=3.\left(3k^2+2k+2k\right)+4+3k+2=3.\left(3k^2+2k+2k+k\right)+6\)
\(=3.\left(3k^2+5k\right)+3.2=3.\left(3k^2+5k+2\right)\) chia hết cho 3
Như vậy tích 2 số tự nhiên liên tiếp luôn chia hết cho 3 hoặc chia 3 dư 2.
Mà \(\left(-3\right)^{20}+1=3^{20}+1\) chia 3 dư 1
Vậy \(\left(-3\right)^{20}+1\) không phải tích 2 số tự nhiên liên tiếp.

Gọi 2 số tự nhiên liên tiếp là n và n+1
Gọi d là UCLN (n , n+1 ) [ d thuộc N* ]
Ta có n : d => [( n +1 )-n ] : d
n+1 : d
=> 1 : d => d = 1
UCLN ( n , n + 1 ) =1
vậy 2 số tự nhiên liên tiếp là 2 số nguyên tố cùng nhau
tich nha
Gọi số thứ nhất là n, số thứ hai là n+1, ƯC﴾n,n+1﴿=a
Ta có: n chia hết cho a﴾1﴿
n+1 chia hết cho a﴾2﴿
Từ ﴾1﴿ và ﴾2﴿ ta được: n+1‐n chia hết cho a
=> 1 chia hết cho a
=> a=1
=> ƯC﴾n,n+1﴿=1
=> n và n+1 là hai số nguyên tố cùng nhau.
Vậy 2 số tự nhiên liên tiếp là hai số nguyên tố cùng nhau

Chọn B.
Để tích các số chấm xuất hiện ở năm lần gieo là một số tự nhiên có tận cùng bằng 5 thì phải có ít nhất một lần ra mặt 5 chấm và các mặt khác ra mặt lẻ. Do đó xác suất cần tìm bằng
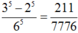

Phân tích 19656 ra thừa số nguyên tố ta có:
19656=23.33.7.13=8.27.7.13
Từ đó biểu diễn 19656 dưới tích của 3 thừa số:
19656= (13.2).27.(7.4) ( 1 số bạn thắc mắc 2 và 4 lấy ở đâu ra thực chất nó từ 8=2.4)
=> 19656=27.26.28
Vậy 3 số tự nhiên đó bằng 26;27;28
phân tích 19656 ra thừa số nguyên tố
19656 = 2^3. 3^3. 7.13 = 8. 27 . 7.13
từ đó biểu diễn 19656 dưới dạng tích của 3 thừa số
19656 = (13.2) . 27. (7.4) = 26. 27. 28
vậy 3 số tự nhiên liên tiếp là 26, 27, 28

Chọn đáp án B
Phương pháp
+) Tính số phần tử của không gian mẫu.
+) Gọi A là biến cố: “Trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp”
=> A “Trong 3 số tự nhiên được chọn có 2 số tự nhiên liên tiếp”.
+) Tính số phần tử của biến cố A .
+) Tính xác suất của biến cố A , từ đó tính xác suất biến cố A.
Cách giải
Chọn ngẫu nhiên 3 số tự nhiên ⇒ n Ω = C 2019 3
Gọi A là biến cố: “Trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp”
=> A : “Trong 3 số tự nhiên được chọn có 2 số tự nhiên liên tiếp”.
Số cách chọn 3 trong 2019 số, trong đó có 2 số tự nhiên liên tiếp, có 2018.2017 cách (có bao gồm các bộ 3 số tự nhiên liên tiếp).
Số cách cả 3 số tự nhiên liên tiếp, có 2017 cách.
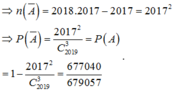
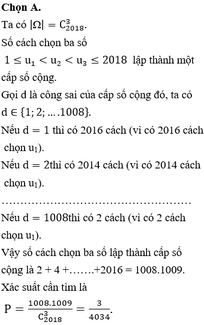

Không tồn tại 2 số đó
ko co 2 so do mo