Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mỗi cặp sắp thứ tự gồm hai điểm (A; B) cho ta một vectơ có điểm đầu A và điểm cuối B và ngược lại.
Như vậy, mỗi vectơ có thể xem là một chỉnh hợp chập 2 của tập hợp 6 điểm đã cho.
Suy ra có A 6 2 = 30 cách.
Chọn đáp án D.

Đáp án A
Số cách lấy ra 4 ứng viên bất kỳ từ 16 ứng viên là ![]() cách.
cách.
- Gọi A là biến cố “4 ứng viên lấy được có đúng một ứng viên 10 tuổi và không quá hai ứng viên 12 tuổi”. Ta xét ba khả năng sau:
- Số cách lấy 1 10 tuổi, 3 11 tuổi là: ![]()
- Số cách lấy 1 10 tuổi, 2 11 tuổi, 1 12 tuổi là: ![]()
- Số cách lấy 1 10 tuổi, 1 11 tuổi, 2 12 tuổi là: ![]()
Xác suất của biến cố A là 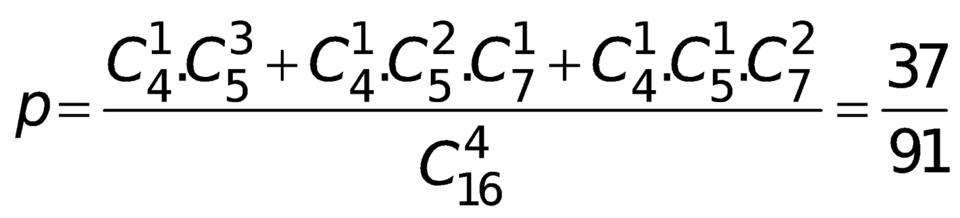 .
.

Đáp án B.
Tổng số trận đấu trong giải đấu là: ![]()
Sau mỗi trận hòa, tổng số điểm 2 đội nhận được là 1.2 =2.
Sau mỗi trận không hòa, tổng số điểm 2 đội nhận được là 3 + 0 = 3.
Tổng số điểm của tất cả các đội sau khi kết thúc giải đấu là:
65.2 + (182 – 65).3 = 481.

iệc chọn 4 bóng đèn mắc nối tiếp chính là việc chọn lấy 4 bóng đèn khác nhau trong tập hợp 6 bóng đèn và sắp xếp chúng theo thứ tự và chính là chỉnh hợp chập 4 của 6.
Vậy có A 6 4 = 6 . 5 . 4 . 3 = 360 (cách).

Mỗi cách mắc nối tiếp 4 bóng đèn được chọn từ 6 bóng đen khác nhau đã cho là một chỉnh hợp chập 4 của 6 bóng đèn đã cho. Do đó số các cách mắc là:
A46 = 360 (cách).

1.
Gọi số đó là \(\overline{abcd}\)
- Nếu d=0 \(\Rightarrow abc\) có \(A_7^3=210\) cách chọn và hoán vị
- Với \(d\ne0\Rightarrow d\) có 4 cách chọn, bộ \(abc\) có \(A_7^3-A_6^2=180\) cách \(\Rightarrow180.4=720\) cách
Vậy có \(210+720=930\) số thỏa mãn
2.
Số cách thỏa mãn: \(A_{11}^5=55440\)
3.
Số cách lấy 3 bi không quan tâm xanh đỏ: \(C_8^1.C_{10}^2=360\)
Số cách lấy toàn bi đỏ: \(C_5^1C_6^2=75\)
Số cách lấy toàn bi xanh: \(C_3^1C_4^2=18\)
Số cách thỏa mãn: \(360-\left(75+18\right)=...\)