
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(A=sin^210^0+sin^280^0+cos^220^0+sin^270^0\)
\(=sin^210^0+cos^210^0+sin^270^0+sin^270^0\)
\(=2\cdot sin^270^0+1\)
b: \(=sin^215^0+sin^275^0+sin^235^0+sin^255^0\)
\(=sin^215^0+cos^215^0+sin^235^0+cos^235^0\)
=1+1
=2

\(A=sin^210^0+sin^280^0+cos^220^0+sin^270^0\)
\(=sin^210^0+cos^210^0+sin^270^0+sin^270^0\)
\(=2sin^270^0+1\)
\(B=sin^215^0+sin^275^0+sin^235^0+sin^255^0\)
\(=sin^215^0+cos^215^0+sin^235^0+cos^235^0\)
=1+1
=2


a. x2 - 11 = \(x^2-\left(\sqrt{11}\right)^2=\left(x-\sqrt{11}\right)\left(x+\sqrt{11}\right)\)
b. x2 - 5 = \(x^2-\left(\sqrt{5}\right)^2=\left(x-\sqrt{5}\right)\left(x+\sqrt{5}\right)\)
c. x2 - 7 = \(x^2-\left(\sqrt{7}\right)^2=\left(x+\sqrt{7}\right)\left(x-\sqrt{7}\right)\)

Ta có: \(\sin^2\alpha+\cos^2\alpha=1\)
\(\Leftrightarrow\sin^2=1-\dfrac{16}{49}=\dfrac{33}{49}\)
Ta có: \(4\cdot\cos^2\alpha-3\cdot\sin^2\alpha\)
\(=4\cdot\dfrac{16}{49}-3\cdot\dfrac{33}{49}\)
\(=\dfrac{64-99}{49}=-\dfrac{5}{7}\)
`cos^2α=16/49`
`sin^2α+cos^2α=1`
`<=>sin^2α+(4/7)^2=1`
`<=>sin^2α=33/49`
`4cos^2α-3sin^2α=4. 16/49 - 3. 33/49 = -5/7`

\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7=23-8\sqrt{7}\)

\(M=3^5+3^6+3^7\)
\(=3^5\left(1+3+3^2\right)=3^5.13⋮13\)
Bài này mà bạn bảo của lớp 9 á
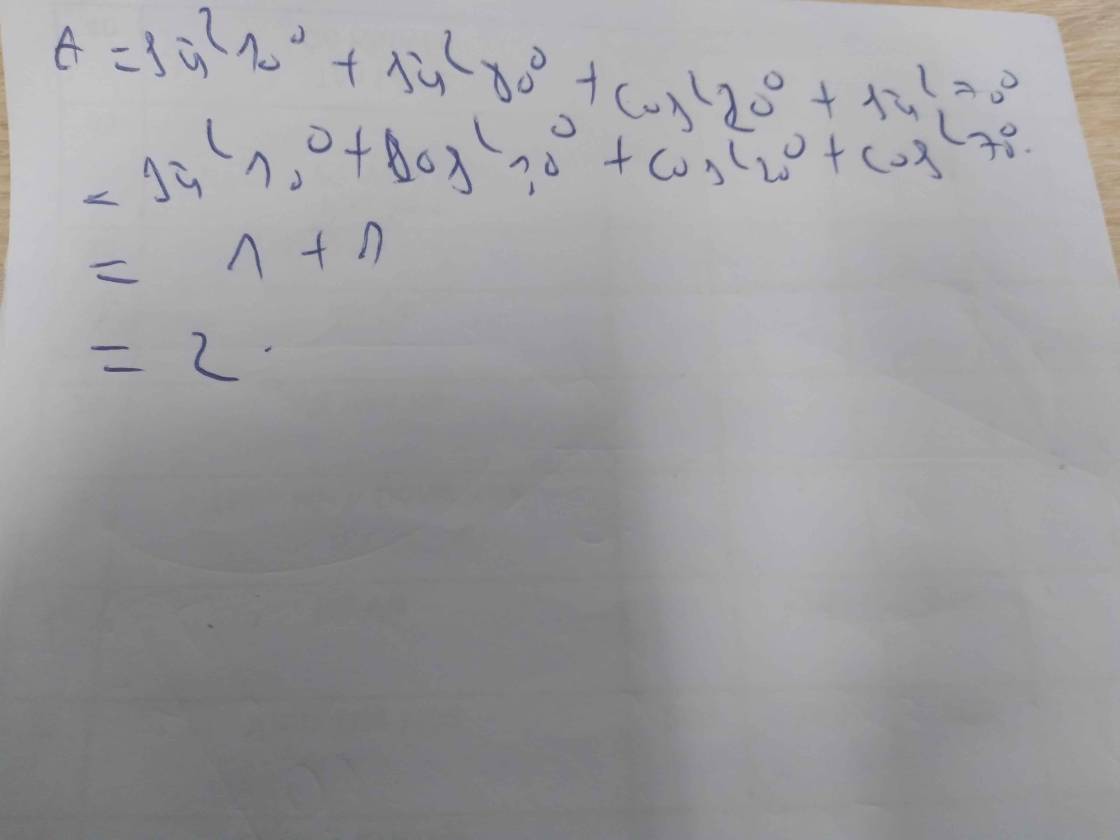
\(\left(\frac{15}{7}\right)^2+\left(\frac{20}{7}\right)^2=\frac{225}{49}+\frac{400}{49}=\frac{625}{49}\)