ND
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
18 tháng 12 2017
Lời giải:
Thể tích của chiếc hộp đó là:
\(V=x.x.h=500\Leftrightarrow x^2h=500\)
\(\Rightarrow h=\frac{500}{x^2}\)
Diện tích của chiếc hộp đó bao gồm diện tích một đáy và 4 mặt bao quanh:
\(S(x)=x^2+4xh\)
\(\Leftrightarrow S(x)=x^2+4x.\frac{500}{x^2}=x^2+\frac{2000}{x}\)
Đến đây có thể sử dụng đạo hàm rồi lập bảng biến thiên để tìm S(x) min, hoặc sử dụng cách ngắn gọn là:
Áp dụng BĐT Cô- si: \(x^2+\frac{2000}{x}=x^2+\frac{1000}{x}+\frac{1000}{x}\geq 3\sqrt[3]{x^2.\frac{1000}{x}.\frac{1000}{x}}=300\)
Hay \(S(x)\geq 300\)
Dấu bằng xảy ra khi \(x^2=\frac{1000}{x}\Leftrightarrow x=10\)
Đáp án B
Q
31 tháng 3 2017
Kí hiệu x, y thứ tự là chiều dài và chiều rộng của hình chữ nhật (0 < x, y < 16). Khi đó x + y = 8. Theo bất đẳng thức Cô-si, ta có : 8 = x + y ≥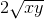 
⇔ xy ≤ 16.
xy =16 ⇔ x = y = 4. Vậy diện tích hình chữ nhật lớn nhất bằng 16 cm2 khi x = y = 4(cm), tức là khi hình chữ nhật là hình vuông.
27 tháng 12 2018
Bài 1: Thực hiện phép tính
a)136 - (2 . 52 + 23 . 3)
= 136 - (104 + 69)
= 136 - 173
= -37
b) (-243) + (-12) + (+243) + (-38) + (10)
= [(-243) + (+243)] + (-12) + (-38) + (10)
= 0 + (-40)
= -40
27 tháng 12 2018
Bài 2 : Tìm x ∈ N, biết:
a) 6 . (x-81) = 54
⇒ x - 81 = 54 : 6
⇒ x - 81 = 9
x = 81 + 9
x = 90
Vậy : x = 90
b) 18 - (x-4) = 32
⇒ x - 4 = 18 - 32
⇒ x - 4 = -14
x = -14 + 4
x = -10
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 5 2019
Cách làm bài này, bạn tự xử nhé:
- Nhận thấy ngay 1 tính chất quan trọng dựa vào hình học phẳng: điểm M nhìn đoạn AB dưới 1 góc vuông nên M thuộc mặt cầu (S) có tâm là trung điểm AB, bán kính \(R=\frac{AB}{2}\), gọi I là trung điểm AB thì I là tâm mặt cầu
\(\Rightarrow M\) thuộc giao tuyến của mặt cầu (S) và (P)
Bài toán trở thành tìm điểm trên đường tròn sao cho k/c tới 1 điểm cố định là lớn nhất \(\Rightarrow\) nó là giao điểm của đường nối tâm và điểm cố định với đường tròn
Vậy ta lập pt mặt phẳng (Q) chứa C và I, vuông góc (P)
Giao điểm của (P), (Q), (S) sẽ là M cần tìm (luôn có 2 giao điểm, 1 cái min 1 cái max)
Q
7 tháng 6 2017
a) \(2^{x+4}+2^{x+2}=5^{x+1}+3\cdot5^x\)
\(\Rightarrow2^x+2^4+2x^x+2^2=5^x\cdot x+3\cdot5^x\)
\(\Leftrightarrow2^x+16+2^x\cdot4=5\cdot5^x+3\cdot5^x\)
\(\Leftrightarrow16\cdot2^x+4\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot2^x=8\cdot5^x\)
\(\Leftrightarrow20\cdot\left(\dfrac{2}{5}\right)^x=8\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\dfrac{2}{5}\)
\(\Leftrightarrow\left(\dfrac{2}{5}\right)^x=\left(\dfrac{2}{5}\right)^1\)
\(\Rightarrow x=1\)
16 tháng 12 2019
Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không k "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
P/s: Đây là diễn đàn để học, not phải nơi quảng cáo. Oke!
#HuyềnAnh#
26 tháng 3 2016
gợi ý :
Tìm giá trị của \(m\) để hàm số có cực đại ,cực tiểu .
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 6 2020
8.
\(\int3^xdx=\frac{3^x}{ln3}+C\)
9.
\(V=\frac{1}{3}S.h\Rightarrow h=\frac{3V}{S}=\frac{2\sqrt{6}}{3}\)
10.
\(V=\frac{4}{3}\pi R^3\Rightarrow R=\sqrt[3]{\frac{3V}{4\pi}}=\sqrt[3]{\frac{3.36\pi}{4\pi}}=\sqrt[3]{27}=3\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 6 2020
4.
\(u_2=u_1q\Rightarrow u_1=\frac{u_2}{q}=\frac{8}{3}\)
5.
\(log_2\left(x-5\right)=3\Rightarrow x-5=8\Rightarrow x=13\)
6.
\(AC=a\sqrt{6}\Rightarrow AB=\frac{AC}{\sqrt{2}}=a\sqrt{3}\)
\(\Rightarrow V=AB^3=9\sqrt{3}.a^3\)
7.
\(y'=e^{2x}.\left(2x\right)'=2.e^{2x}\)
1565:5=313
4568:8=571 2135=213500