Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do ABCD là hình thang cân nên AD = BC, AC = BC,
Xét hai tam giác ADC và BCD, ta có: 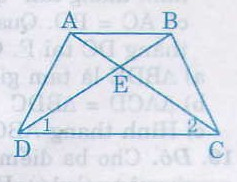
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, , DC là cạnh chung.
Chứng Minh;
Xét tam giác ADC và BCD, có:
AD = BC ( gt )
DC là cạnh chung
AC = BD ( gt )
\(\Rightarrow\)Tam giác ADC = BCD ( c.c.c )
\(\Rightarrow\)Â1 = B1 ( 2 góc Tương ứng )
Mà Góc DAB= CBA ( gt )
\(\Rightarrow\)Â2= B2 ( gt )
\(\Rightarrow\)Tam giác AEB cân tại E
nên EA=EB
mà AC=BD
\(\Rightarrow\)EC=ED A B D C 1 2 2 1 E

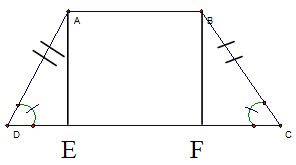
ABCD (AB // DC) LÀ Hình thang cân ta có :
\(\widehat{D}=\widehat{C};AD=BC\)
Xét Δ AED và Δ BFC ta có :
\(\widehat{AED}=\widehat{BFC}=90^o\)
\(\widehat{C}=\widehat{D}=\left(cmt\right)\)
\(AD=BC\left(cmt\right)\)
= > Δ AED = Δ BFC (cạnh huyền – góc nhọn)
= > DE = CF

a. Xét tam giác HCD cóHN=DN;HM=CM
=> MN là đường trung bình của tam giác HCD => MN//DC
=> DNMC là hình thang
b. Ta có MN là đường trung bình của tam giác HCD => MN=1/2CD
Mà AB=1/2CD => AB =MN
Do MN//CD và AB//CD => AB//MN
Xét tứ giác ABMN có AB//MN; AB=MN
=> ABMN là hình bình hành
c.Ta có MN//CD mà CD vg AD
=> MN vg AD
Xét tam giác ADM có DH và MN là 2 đường cao của tam giác
Mà chúng cắt nhau tại N nên N là trực tâm của tam giác ADM
=> AN là đường cao của tam giác ADM
=> AN vg DM
Do ABMN là hình bình hành nên AN//BM
=> BM vg DM => BMD =90*

Bài giải:
Do ABCD là hình thang cân nên AD = BC, AC = BC, ˆD=ˆCD^=C^
Xét hai tam giác ADC và BCD, ta có: 
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra ˆC1=ˆD1C1^=D1^
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, ˆD=ˆCD^=C^ , DC là cạnh chung.

Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.

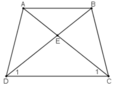
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.

Vì hình thang ABCD cân
AD = BC;
Ĉ = D̂
Xét hai tam giác vuông AED và BFC có:
AD = BC
Ĉ = D̂
⇒ ΔAED = ΔBFC (cạnh huyền – góc nhọn)
⇒ DE = CF.

Do ABCD là hình thang cân nên AD = BC, AC = BC,
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, , DC là cạnh chung.
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.
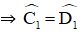
Xét ΔABD và ΔBAC có:
AB: cạnh chung
^A=^B(gt)
AD=BC(gt)
=>ΔABD = ΔBAC(c.g.c)
=>^ABD=^BAC
=>ΔEAB cân tại E
=>AE=EB
Có: AC=AE+EC
BD=BE+ED
Mà AC=BD(gt); AE=BE(cmt)
=>ED=EC
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra \(\widehat{C_1}=\widehat{D_1}\)
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB