NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 2 2021
Ta có : \(\dfrac{5x-150}{50}+\dfrac{5x-102}{49}+\dfrac{5x-56}{48}+\dfrac{5x-12}{47}+\dfrac{5x-660}{46}=0\)
\(\Leftrightarrow\dfrac{5x-150}{50}-1+\dfrac{5x-102}{49}-2+\dfrac{5x-56}{48}-3+\dfrac{5x-12}{47}-4+\dfrac{5x-660}{46}+10=0\)
\(\Leftrightarrow\dfrac{5x-200}{50}+\dfrac{5x-200}{49}+\dfrac{5x-200}{48}+\dfrac{5x-200}{47}+\dfrac{5x-200}{46}=0\)
\(\Leftrightarrow\left(5x-200\right)\left(\dfrac{1}{50}+\dfrac{1}{49}+\dfrac{1}{48}+\dfrac{1}{47}+\dfrac{1}{46}\right)=0\)
\(\Leftrightarrow5x-200=0\)
\(\Leftrightarrow x=40\)
Vậy ...
9 tháng 2 2021
Ta có: \(\dfrac{5x-150}{50}+\dfrac{5x-102}{49}+\dfrac{5x-56}{48}+\dfrac{5x-12}{47}+\dfrac{5x-660}{46}=0\)
\(\Leftrightarrow\dfrac{5x-150}{50}-1+\dfrac{5x-102}{49}-2+\dfrac{5x-56}{48}-3+\dfrac{5x-12}{47}-4+\dfrac{5x-660}{46}+10=0\)
\(\Leftrightarrow\dfrac{5x-200}{50}+\dfrac{5x-200}{49}+\dfrac{5x-200}{48}+\dfrac{5x-200}{47}+\dfrac{5x-200}{46}=0\)
\(\Leftrightarrow\left(5x-200\right)\left(\dfrac{1}{50}+\dfrac{1}{49}+\dfrac{1}{48}+\dfrac{1}{47}+\dfrac{1}{46}\right)=0\)
mà \(\dfrac{1}{50}+\dfrac{1}{49}+\dfrac{1}{48}+\dfrac{1}{47}+\dfrac{1}{46}>0\)
nên 5x-200=0
\(\Leftrightarrow5x=200\)
hay x=40
Vậy: S={40}
1 tháng 1 2018
\(pt\Leftrightarrow\frac{5x-150}{50}+\frac{5x-102}{49}+\frac{5x-56}{48}+\frac{5x-12}{47}+\frac{5x-16}{46}-14=0\)
\(\Leftrightarrow\frac{5x-150}{50}-1+\frac{5x-102}{49}-2+\frac{5x-56}{48}-3+\frac{5x-12}{47}-4+\frac{5x-16}{46}-4=0\)
\(\Leftrightarrow\frac{5x-200}{50}+\frac{5x-200}{49}+\frac{5x-200}{48}+\frac{5x-200}{47}+\frac{5x-200}{46}=0\)
\(\Leftrightarrow\left(5x-200\right)\left(\frac{1}{50}+\frac{1}{49}+\frac{1}{48}+\frac{1}{47}+\frac{1}{46}\right)=0\)
Do \(\frac{1}{50}+\frac{1}{49}+\frac{1}{48}+\frac{1}{47}+\frac{1}{46}\ne0\) nên \(5x-200=0\Rightarrow x=\frac{200}{5}=40\)
Vậy x= 40
KT
1 tháng 1 2018
\(\frac{5x-150}{50}+\frac{5x-102}{49}+\frac{5x-56}{48}+\frac{5x-12}{47}+\frac{5x-660}{46}=0\)
\(\Leftrightarrow\)\(\left(\frac{5x-150}{50}-1\right)+\left(\frac{5x-102}{49}-2\right)+\left(\frac{5x-56}{48}-3\right)+\left(\frac{5x-12}{47}-4\right)+\left(\frac{5x-660}{46}+10\right)=0\)
\(\Leftrightarrow\)\(\frac{5x-200}{50}+\frac{5x-200}{49}+\frac{5x-200}{48}+\frac{5x-200}{47}+\frac{5x-200}{46}=0\)
\(\Leftrightarrow\)\(\left(5x-200\right)\left(\frac{1}{50}+\frac{1}{49}+\frac{1}{48}+\frac{1}{47}+\frac{1}{46}\right)=0\)
\(\Leftrightarrow\)\(5x-200=0\)
\(\Leftrightarrow\)\(5x=200\)
\(\Leftrightarrow\)\(x=40\)
Vậy x = 40
PT
1
CM
18 tháng 9 2018
2x + x + 12 = 0
⇔ 3x + 12 = 0
⇔ 3x = -12
⇔ x = -12 : 3
⇔ x = -4
Vậy phương trình đã cho có nghiệm duy nhất x = -4
PT
1
PT
1
CM
16 tháng 3 2017
2x + x - 12 = 0 ⇔ 3x - 12 = 0 ⇔ 3x = 12 ⇔ x = 4
Vậy phương trình có tập nghiệm S = {4}.
7 tháng 3 2021
a \(\Leftrightarrow3x^2+9x+4x+12=0\Leftrightarrow3x\left(x+3\right)+4\left(x+3\right)=0\Leftrightarrow\left(x+3\right)\left(3x+4\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\3x+4=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-\dfrac{4}{3}\end{matrix}\right.\)
DT
Đỗ Thanh Hải
CTVVIP
7 tháng 3 2021
\(3x^2+13x+12=0\)
\(\Leftrightarrow3\left(x^2+\dfrac{13}{3}x+4\right)=0\Leftrightarrow x^2+\dfrac{13}{3}x+4=0\)
\(\Leftrightarrow x^2+3x+\dfrac{4}{3}x+4=0\)
\(\Leftrightarrow x\left(x+3\right)+\dfrac{4}{3}\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+\dfrac{4}{3}\right)\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{4}{3}\\x=-3\end{matrix}\right.\)
NK
3
T
20 tháng 2 2020
x^3 - x^2 - 21x + 45 = 0
=>x^3 + 5x^2 - 6x^2 - 30x + 9x + 45 = 0
=> x^2(x + 5) - 6x(x + 5) + 9(x + 5) = 0
=> (x^2 - 6x + 9)(x + 5) = 0
=> (x - 3)^2(x + 5) = 0
=> x - 3 = 0 hoặc x + 5 = 0
=> x = 3 hoặc x = -5
20 tháng 2 2020
Ta có: x3−x2+x−1=0
⇔x2(x−1)+(x−1)=0
⇔(x−1)(x2+1)=0(1)
Ta có: x2≥0∀x
⇒x2+1≥1≠0∀x(2)
Từ (1) và (2) suy ra x−1=0
⇔x=1Ta có: x3−x2+x−1=0
⇔x2(x−1)+(x−1)=0
⇔(x−1)(x2+1)=0(1)
Ta có: x2≥0∀x
⇒x2+1≥1≠0∀x(2)
Từ (1) và (2) suy ra x−1=0
⇔x=1
TT
6
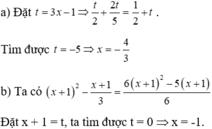
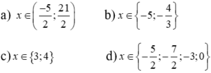
Đề bài thiếu gì đó thì phải