
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{x\left(x+2\right)}=\frac{20}{41}\)
\(\frac{1}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{x\left(x+2\right)}\right)=\frac{20}{41}\)
\(\frac{1}{2}\left(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{x}-\frac{1}{x+2}\right)=\frac{20}{41}\)
\(\frac{1}{2}\left(1-\frac{1}{x+2}\right)=\frac{20}{41}\)
\(\frac{1}{2}.\frac{x+1}{x+2}=\frac{20}{41}\)
\(\frac{x+1}{x+2}=\frac{20}{41}:\frac{1}{2}\)
\(\frac{x+1}{x+2}=\frac{40}{41}\)
\(x+1=40
\)
\(x=40-1\)
\(x=39\)
Đúng thì ****

\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{x\left(x+2\right)}=\frac{20}{41}\)
\(\Leftrightarrow1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{x}-\frac{1}{x+2}=\frac{20}{41}\)
\(\Leftrightarrow1-\frac{1}{x+2}=\frac{21}{41}\)
\(\Leftrightarrow\frac{1}{x+2}=1-\frac{21}{41}\)
\(\Leftrightarrow\frac{1}{x+2}=\frac{20}{41}\)
\(\Leftrightarrow20\left(x+2\right)=41\)
\(\Leftrightarrow x-2=\frac{41}{20}\)
\(\Leftrightarrow x=\frac{41}{20}+2\)
\(\Leftrightarrow x=\frac{81}{20}\)
\(\frac{1}{1.3}+...+\frac{1}{a\left(a+2\right)}=\frac{1}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+....+\frac{2}{a\left(a+2\right)}\right)=\frac{1}{2}\left(1-\frac{1}{3}+....-\frac{1}{a+2}\right)\)
\(=\frac{1}{2}\left(1-\frac{1}{a+2}\right)=\frac{20}{41}\Rightarrow a+2=41\Leftrightarrow a=39\)

Ta có :
\(\dfrac{1}{2}\)(\(\dfrac{1}{1}\)-\(\dfrac{1}{3}\)+\(\dfrac{1}{3}\)-\(\dfrac{1}{5}\)+\(\dfrac{1}{5}\)-\(\dfrac{1}{7}\)+...+\(\dfrac{1}{x}\)-\(\dfrac{1}{x+2}\))=\(\dfrac{20}{41}\)
\(\dfrac{1}{2}\)(\(\dfrac{1}{3}\)-\(\dfrac{1}{x+2}\))=\(\dfrac{20}{41}\)
\(\dfrac{1}{3}\)-\(\dfrac{1}{x+2}\)=\(\dfrac{40}{41}\)
\(\dfrac{1}{x+2}\)=\(\dfrac{1}{3}\)-\(\dfrac{40}{41}\)

Ta có: \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{x\left(x+2\right)}=\dfrac{20}{41}\)
\(\Leftrightarrow\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{x\left(x+2\right)}=\dfrac{40}{41}\)
\(\Leftrightarrow1-\dfrac{2}{x+2}=\dfrac{40}{41}\)
\(\Leftrightarrow\dfrac{2}{x+2}=\dfrac{1}{41}\)
Suy ra: x+2=82
hay x=80

=1/2*(1-1/3+1/3-1/5+....+1/x+1/x+2)
=1/2*(1-1/x+2)
=>1/2*x+1/x+2=20/21
Đến đó đưa về giống tìm x nha

\(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2025\cdot2016}\\ =\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2025}-\dfrac{1}{2026}\\ =\dfrac{1}{1}-\dfrac{1}{2026}=\dfrac{2025}{2026}\\ B=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{99\cdot101}\\ =\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{101}\\ =\dfrac{1}{1}-\dfrac{1}{101}=\dfrac{100}{101}\\ C=\dfrac{5}{1\cdot3}+\dfrac{5}{3\cdot5}+\dfrac{5}{5\cdot7}+...+\dfrac{5}{99\cdot101}\\ =\dfrac{5}{2}\cdot\left(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\\ =\dfrac{5}{2}\cdot\left(\dfrac{1}{1}-\dfrac{1}{101}\right)=\dfrac{5}{2}\cdot\dfrac{100}{101}=\dfrac{250}{101}\)
\(D=\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{9900}\\ =\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{99\cdot100}\\ =\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ =\dfrac{1}{1}-\dfrac{1}{100}=\dfrac{99}{100}\)

\(1/1.3+1/3.5+1/5.7+...+1/n.(n+2)<2003/2004\)
Ta có :=2/2.(1/1.3+1/3.5+1/5.7+...+1/n.(n+2)
=1/2.(2/1.3+2/3.5+2/5.7+...+2/n.(n+2)
=1/2.(1-1/3+1/3-1/5+1/5-1/7+...+1/n-1/n+2)
=1/2.(1-1/n+2)
=1/2.(n+2/n+2-1/n+2)
=1/2.(n+2-1/n+2)
=1/2.n+1/n+2
=n+1/(n+2).2
Vì: n+1/(n+2).2<2003/2004
Suy ra:n+1/(n+2).2=x/2004
Suy ra:(n+2).2=2004
n+2 =1002
n =1000
Vậy n bằng 1000
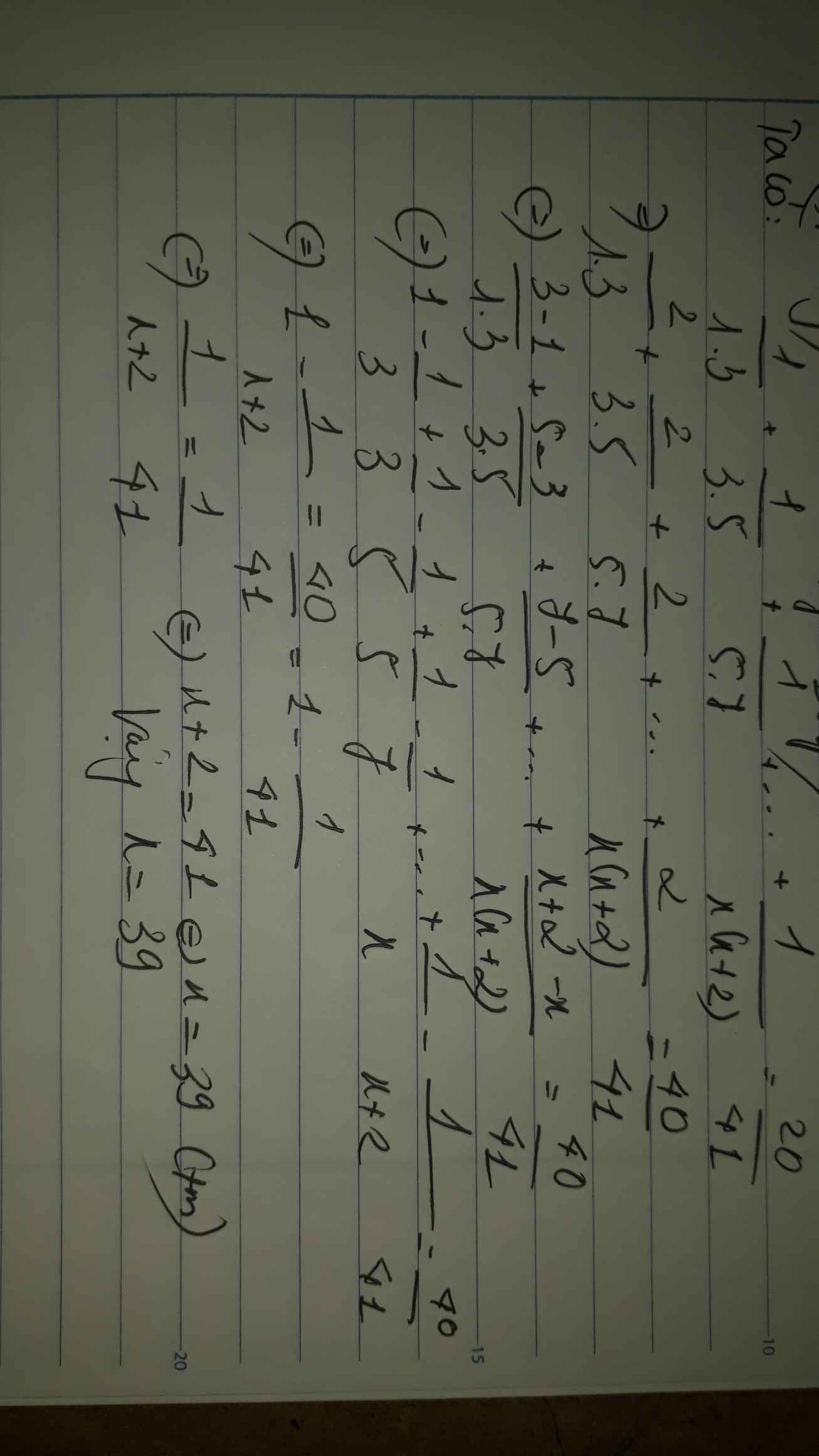
\(\frac{1}{1\cdot3}+\frac{1}{3\cdot5}+...+\frac{1}{n\left(n+2\right)}=\frac{20}{41}\)
\(\left(\frac{1}{1\cdot3}+\frac{1}{3\cdot5}+...+\frac{1}{n\left(n+2\right)}\right)\cdot2=\frac{20}{41}\cdot2\)
\(\frac{2}{1\cdot3}+\frac{2}{3\cdot5}+...+\frac{2}{n\left(n+2\right)}=\frac{40}{41}\)
\(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{n}-\frac{1}{n+2}=\frac{40}{41}\)
\(1-\frac{1}{n+2}=\frac{40}{41}\)
\(\frac{1}{n+2}=1-\frac{40}{41}\)
\(\frac{1}{n+2}=\frac{1}{41}\)
\(\Rightarrow n+2=41\)
\(n=41-2\)
\(n=39\)