K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 10 2023
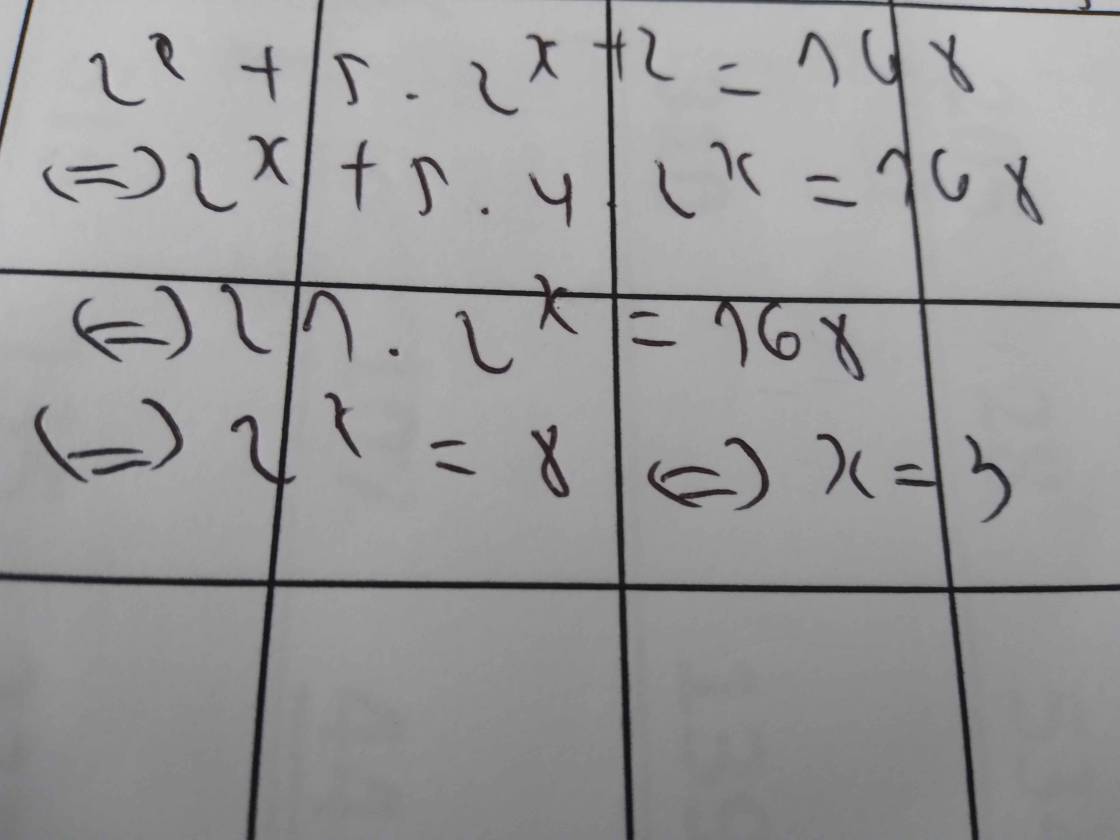
\(2^x+5\cdot2^{x+2}=168\)
=>\(2^x+20\cdot2^x=168\)
=>\(21\cdot2^x=168\)
=>\(2^x=8=2^3\)
=>x=3
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
16 tháng 10 2023
\(2^x+5.2^{x+2}=168\\ \Leftrightarrow2^x.\left(1+5.2^2\right)=168\\ \Leftrightarrow2^x.21=168\\ \Leftrightarrow2^x=\dfrac{168}{21}=8=2^3\\ Vây:x=3\)
LN
18 tháng 10 2023
2x+5.2x+2=168⇔2x.(1+5.22)=168⇔2x.21=168⇔2x=16821=8=23
Vây:x=3
HT
1
DD
8 tháng 10 2016
\(10^a+168=b^2\)
\(\text{Xét a=0}\)
\(\Rightarrow10^0+168=1+168=169=13^2\)
\(\Rightarrow a=0;b=0\)
\(\text{Xét a khác 0}\)
\(\text{10^a có tận cùng =0}\)
\(\Rightarrow10^a+168\)\(\text{có tận cung=8(k phải là số chính phương)}\)
\(\Rightarrow\)\(\text{k có b}\)
\(\text{Vậy chỉ có a=0;b=2}\)
NT
2
6 tháng 4 2019
\(\frac{-4}{8}=\frac{x}{-10}=\frac{-7}{y}\)
Vậy x = -4 . -10 : 8 = 5
=> Y = -10 . 7 : 5 = 14
Câu 2 ( CHỊU) BÓ TAY
KN
6 tháng 4 2019
\(A=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{10^2}\)
\(\Rightarrow A< \frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{10}\)
\(\Rightarrow A< \frac{1}{10}+\frac{1}{10}+\frac{1}{10}+...+\frac{1}{10}\) ( 9 số hạng \(\frac{1}{10}\))
\(\Rightarrow A< \frac{9}{10}< 1\)
Vậy \(A< 1\left(đpcm\right)\)
L
4
16 tháng 9 2018
Ta có : \(10^x\)tận cùng bằng 0
\(\Rightarrow10^x+48\)tận cùng bằng 8
Mà \(y^2\)chỉ có thể tận cùng bằng 0; 1; 4; 5; 6; 9
Nên ko tồn tại x, y thỏa mãn yêu cầu bài toán
HN
23 tháng 8 2017
bài 1:
\(a,21^{15}=3^{15}\times7^{15}\)
\(27^5\times49^8=3^{15}\times7^{16}\)
Vậy: \(21^{15}< 27^5\times49^8\)
\(b,27^5=3^{15}\)
\(243^3=3^{15}\)
Vậy: \(27^5=243^3\)
Bài 2:
\(10^x+48=48^y\)
=100..0+48=\(48^y\)
=100...048=\(48^y\)
còn các bước tiếp mik chưa nghĩ ra cậu suy nghĩ thêm nhé
ta có : 168 không là số bình phương vậy 10^x sẽ không là số bình phương
mà y^2 là bình phương
vì 10^x + 168 = 10..0168 mà số bình phương ko có tận cùng là : 2 ; 3 ; 7 ; 8 nên phép tính đó là sai