Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thời gian ngắn nhất khi vật đi với vận tốc lớn nhất, do đó nó sẽ dao động quanh VTCB từ toạ độ \(-\dfrac{A\sqrt 2}{2}\) đến \(\dfrac{A\sqrt 2}{2}\)
Ta vẽ véc tơ quay ra, sẽ tìm được góc quay là \(90^0\)
Vậy thời gian là: \(t=\dfrac{90}{360}T=\dfrac{T}{4}=\dfrac{1}{4f}\)
Chọn B.

Trong 1 chu kì, thời gian mà động năng nhỏ hơn (hoặc không nhỏ hơn) thế năng là: T/2 = 2/2 = 1s
Chọn B.

1) \(W_đ=W_t\Rightarrow W=W_đ+W_t=2W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=2.\dfrac{1}{2}kx^2\)
\(\Rightarrow x = \pm\dfrac{A}{\sqrt 2}\)
Như vậy, trong 1 chu kì có 4 lần động năng bằng thế năng được biểu diễn bằng véc tơ quay như sau.
x A -A O M N P Q
Đó là các vị trí ứng với véc tơ quay đi qua M, N, P, Q
Như vậy, thời gian giữa 2 lần liên tiếp động năng bằng thế năng là 1/4T
\(\Rightarrow \dfrac{T}{4}=0,2\Rightarrow T = 0,8s\)
\(W_đ=nW_t\)
\(\Rightarrow W = W_đ+W_t=nW_t+W_t=(n+1)W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=(n+1).\dfrac{1}{2}kx^2\)
\(\Rightarrow \dfrac{A}{x}=\pm\sqrt{n+1}\)
\(\Rightarrow \dfrac{\omega^2. A}{-\omega^2.x}=\pm\sqrt{n+1}\)
\(\Rightarrow \dfrac{a_{max}}{a}=\pm\sqrt{n+1}\)

Ta có: \(W_đ=W_t\Rightarrow x =\pm\dfrac{A}{\sqrt 2}\)
Như vậy, để \(W_t < W_đ\) thì: \(|x| <\dfrac{A}{\sqrt 2}\)
Biểu điễn bằng véc tơ quay, ta tìm đc khoảng thời gian tương ứng này bằng T/4 = 2/4 = 0,5s
Chọn A.

+ Khi \(W_đ=3W_t\Rightarrow W=4W_t\Rightarrow x=\pm\frac{A}{2}\)
+ Khi \(W_đ=\frac{1}{3}W_t\Rightarrow W=\frac{4}{3}W_t\Rightarrow x=\pm\frac{\sqrt{3}}{2}A\)
Ta có véc tơ quay như sau:
x A/2 A A√3/2 30° M N
Thời gian nhỏ nhất ứng với véc tơ quay từ M đến N.
\(t=\frac{30}{360}T=\frac{1}{12}.2=\frac{1}{6}s\)
\(S=\left(\frac{\sqrt{3}}{2}-\frac{1}{2}\right).10=\left(\sqrt{3}-1\right).5\)
Tốc độ trung bình: \(v=\frac{S}{t}=\left(\sqrt{3}-1\right).30=21,96\)(cm/s)


Thời gian ngắn nhất cần tìm là thời gian chất điểm đi từ 
hoặc 
Quãng đường cần tìm là :


Trong dao động điều hoà, động năng và thế năng biến đổi tuần hoàn với tần số gấp đôi tần số dao động.
Chọn B.

Để tính khoảng thời gian trong một chu kỳ mà động năng nhỏ hơn ba lần thế năng của một vật dao động điều hoà, chúng ta có thể sử dụng công thức sau:
Tổng động năng = 3 * Tổng thế năng
Trong một chu kỳ, tổng động năng bằng tổng thế năng. Vì vậy, ta có:
3 * Tổng thế năng = Tổng thế năng
Từ đó, ta có:
2 * Tổng thế năng = 0
Vậy, khoảng thời gian trong một chu kỳ mà động năng nhỏ hơn ba lần thế năng là 0.
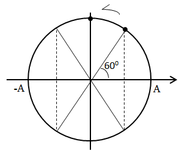
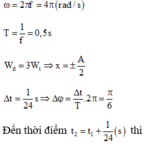

Ta có: \(W_t=3W_đ\)
\(\Rightarrow W=W_đ+W_t=\dfrac{4}{3}W_t\)
\(\Rightarrow x = \pm\dfrac{\sqrt 3}{2}A\)
Để thế năng không nhỏ hơn 3 lần động năng thì \(|x|\le \dfrac{\sqrt 3}{2}A\)
Biểu diễn dao động bằng véc tơ quay:
> x M N P Q 60 0 A -A √3 2 A
Trạng thái trên ứng với véc tơ quay từ M đến N và từ P đến Q.
Góc quay: \(\alpha = 60.4=240^0\)
Thời gian: \(t=\dfrac{240}{360}T=\dfrac{2}{3}T=\dfrac{2}{3f}\)
Chọn B.