Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì d là đường trug trực của AB mà C,D thuộc d nên: AC=BC =>tam giác ACB cân tại C=> Góc CAB= góc CBA (1)
AD=BD=>tam giácABD cân tại D=> Góc DAB= góc DBA (2)
TỪ (1) và

a) Xét tam giác \(AHD\) và tam giác \(AKD\):
\(\widehat{AHD}=\widehat{AKD}\left(=90^o\right)\)
\(AD\) cạnh chung
\(\widehat{HAD}=\widehat{KAD}\) (vì \(AD\) là tia phân giác góc \(A\) của tam giác \(ABC\))
Suy ra \(\Delta AHD=\Delta AKD\) (cạnh huyền - góc nhọn)
\(\Rightarrow AH=AK\).
b) \(\Delta AHD=\Delta AKD\) suy ra \(DH=DK\) suy ra \(D\) thuộc đường trung trực của \(HK\).
\(AH=AK\) suy ra \(A\) thuộc đường trung trực của \(HK\)
suy ra \(AD\) là đường trung trực của \(HK\).
c) Xét tam giác \(AKE\) và tam giác \(AHF\):
\(\widehat{A}\) chung
\(AH=AK\)
\(\widehat{AHF}=\widehat{AKE}\left(=90^o\right)\)
suy ra \(\Delta AKE=\Delta AHF\) (g.c.g)
suy ra \(AE=AF\)
Xét tam giác \(AEF\) có: \(\dfrac{AH}{AE}=\dfrac{AK}{AF}\) suy ra \(HK//EF\).

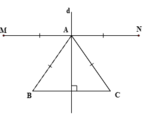
Ta có: B A M ^ = B ^ ( g t ) C A N ^ = C ^ ( g t )
Þ AM // BC; AN // BC (vì có cặp góc so le trong bằng nhau).
Þ 3 điểm M, A, N thẳng hàng (vì qua điểm A chỉ vẽ được một đường thẳng song song với BC).
Vậy MN // BC mà d ⊥ B C nên d ⊥ M N (1)
Ta có: A M = A B ; A N = A C
mà AB = AC (gt) nên AM = AN. (2)
Từ (1) và (2) Þ d là trung trực của MN
