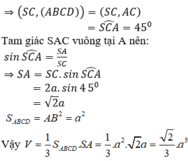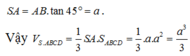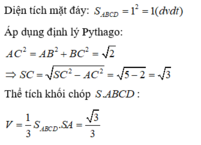Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
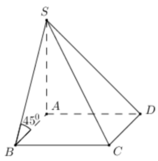
$SA\perp (ABCD)$ nên $45^0=\angle (SB, (ABCD))=\angle (SB, AB)=\widehat{SBA}$
$\Rightarrow SA=AB=5$ (cm)
Thể tích khối chóp $S.ABCD$:
$V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.5.5^2=\frac{125}{3}$ (cm3)

Đáp án C
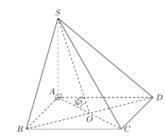
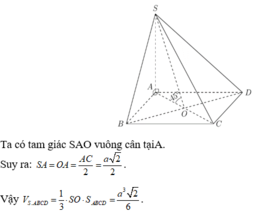
Ta có tam giác SAO vuông cân tạiA.
Suy ra:
S
A
=
O
A
=
A
C
2
=
a
2
2
Vậy : V S . A B C D = 1 3 . S O . S A B C D = a 3 2 6

Đáp án là B

Ta có:
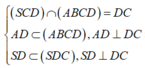
![]()
Gọi cạnh hình vuông là x
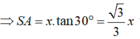
và AC =x 2
![]()
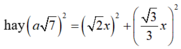
Từ đó ta có x=a 3 . Do đó SA = a
Thể tích khối chóp cần tìm là
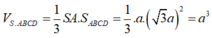
Chọn đáp án B


Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).