Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải:
1.
\((-2x^4y^3z^7)^2(\frac{1}{4}xy^5)(-3x^2yz)^3(\frac{-1}{27}x^3yz^2)\)
\(=(4x^8y^6z^{14})(\frac{1}{4}xy^5)(-27x^6y^3z^3)(-\frac{1}{27}x^3yz^2)\)
\(=(4.\frac{1}{4}.-27.\frac{-1}{27})(x^8.x.x^6.x^3)(y^6.y^5.y^3.y)(z^{14}.z^3.z^2)\)
\(=x^{18}.y^{15}.z^{19}\)
2.
\(=(\frac{-1}{3}.\frac{4}{5}.\frac{-27}{10})(x.x^5.x^2)(y^2.y^6.y)(z.z.z^4)\)
\(=\frac{18}{25}.x^8.y^9.z^6\)
3.
\(=(49.x^{10}y^2z^4)(\frac{-1}{4}.x^3yz^7)(\frac{8}{21}x^5z^4)\)
\(=(49.\frac{-1}{4}.\frac{8}{21})(x^{10}.x^3.x^5)(y^2.y)(z^4.z^7.z^4)\)
\(=\frac{-14}{3}.x^{18}.y^3.z^{15}\)
4.
\(=(\frac{-1}{64}.x^8.y^9.z^{12})(4x^2y^2z^4)(\frac{-5}{3}x^4yz)\)
\(=(\frac{-1}{64}.4.\frac{-5}{3})(x^8.x^2.x^4)(y^9.y^2.y)(z^{12}.z^4.z)\)
\(=\frac{5}{48}.x^{14}.y^{12}.z^{17}\)
5.
\(=(\frac{1}{16}.x^8.y^4z^2)(-8xyz^2).(-\frac{1}{2}x^4yz)\)
\(=(\frac{1}{16}.-8.\frac{-1}{2})(x^8.x.x^4)(y^4.y.y)(z^2.z^2.z)\)
\(=\frac{1}{4}.x^{13}.y^6.z^5\)
B1
a) 3x2y3.(-6x3y )
\(=\left(3.-6\right)\left(x^2.x^3\right)\left(y^3y\right)\)
\(=-18x^5y^{\text{4 }}\)
B2
a), b)
\(A=\left(\frac{-3}{7}x^2y^2z\right).\left(\frac{-42}{9}xy^2z^2\right)\)
\(A=\left(\frac{-3}{7}.\frac{-42}{9}\right)\left(x^2.x\right)\left(y^2.y^2\right)\left(z.z^2\right)\)
\(A=2x^3y^4z^3\) - Bậc 10
Hệ số : 2
c) Thay x = 2 , y = 1 , z = -1 vào biểu thức A , ta có :
\(A=2.2^3.1^4.\left(-1\right)^3\)
\(A=2.8.1.\left(-1\right)\)
A = -16
Vậy , tại x = 2 , y = 1 , z = -1 thì A = -16
1.
\((\frac{1}{3}xy)^2.x^3+\frac{3}{2}(2x)^3(-\frac{7}{4}x^2y^2)-\frac{2}{3}x^5y^2\)
\(=(\frac{1}{9}x^2y^2)x^3+\frac{3}{2}(8x^3)(-\frac{7}{4}x^2y^2)-\frac{2}{3}x^5y^2\)
\(=\frac{1}{9}(x^2.x^3)y^2+(\frac{3}{2}.8.\frac{-7}{4})(x^3.x^2).y^2-\frac{2}{3}x^5y^2\)
\(=\frac{1}{9}x^5y^2-21x^5y^2-\frac{2}{3}x^5y^2=\frac{-194}{9}x^5y^2\)
2.
\(\frac{-2}{5}x^2y(-y^6)+\frac{3}{2}xy(\frac{-1}{15}xy^6)+(-2xy)^2y^5\)
\(=\frac{2}{5}x^2(y.y^6)+(\frac{3}{2}.\frac{-1}{15})(x.x).(y.y^6)+4x^2(y^2.y^5)\)
\(=\frac{2}{5}x^2y^7-\frac{1}{10}x^2y^7+4x^2y^7=\frac{43}{10}x^2y^7\)
3.
\(\frac{3}{7}xy^2z+\frac{1}{2}x^3y^2+\frac{1}{3}x^3y^2-\frac{3}{7}xy^2z\)
\(=(\frac{3}{7}xy^2z-\frac{3}{7}xy^2z)+(\frac{1}{2}x^3y^2+\frac{1}{3}x^3y^2)\)
\(=\frac{5}{6}x^3y^2\)
4.
\(\frac{2}{3}xy^2-\frac{5}{2}yz+\frac{1}{2}xy^2-\frac{2}{3}yz\)
\(=(\frac{2}{3}xy^2+\frac{1}{2}xy^2)-(\frac{5}{2}yz+\frac{2}{3}yz)\)
\(=\frac{7}{6}xy^2+\frac{19}{6}yz\)
5.
\(\frac{3}{2}xy^2z^5-\frac{5}{4}xyz^2+\frac{4}{3}xy^2z^5+\frac{1}{2}xyz^2\)
\(=(\frac{3}{2}xy^2z^5+\frac{4}{3}xy^2z^5)+(\frac{-5}{4}xyz^2+\frac{1}{2}xyz^2)\)
\(=\frac{17}{6}xy^2z^5-\frac{3}{4}xyz^2\)
câu 1: a)M=3x^2-1/2+1+2x-x^2
= 2x^2-3/2+2x
ta có: hạng tử 2x^2 có bậc là 2
hạng tử -3/2 có bậc là 0
hạng tử 2x có bậc là 1
vậy đa thức M có bậc là 2
b) N=3x^2+7x^3-3x^3+6x^3-3x^2-1/5
=10x^3-1/5
ta có: hạng tử 10x^3 có bậc là 3
hạng tử 1/5 có bậc là 0
vậy bậc của đa thức N là 3
câu 2: Q= x^2+y^2+z^2+x^2-y^2+z^2+x^2+y^2-z^2
=3x^2+y^2+z^2
câu 3: P=1/3x^2y+xy^2-xy+1/2xy^2-5xy-1/3x^y
=3/2xy^2-6xy
1)
a) 3x2 –
x + 1 + 2x – x2 = 3x2 + 
x + 1 có bậc 2;
b) 3x2 + 7x3 – 3x3 + 6x3 – 3x2 = 10x3 có bậc 3
2)
Q = x2 + y2 + z2 + x2 - y2 + z2 + x2 + y2 - z2.
Q = (x2 + x2 + x2 ) + (y2 - y2 + y2) + (z2 + z2 - z2)
= 3x2 + y2 + z2.
3)
Thu gọn rồi tính giá trị của đa thức P tại x = 0,5 và y = 1.
Ta có: P =
x2 y + xy2 – xy + 
xy2 – 5xy – 
x2y
P =
x2 y – 
x2y + 
xy2 + xy2 – xy – 5xy = 
xy2 – 6xy
Thay x = 0,5 và y = 1 ta được
P =
. 0,5 . 12 – 6. 0,5 . 1 = 
- 3 =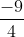 
.
Vậy P =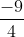
tại x = 0,5 và y = 1.