Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
2 = T = 2 π m k = 2 π m 20 ⇒ m = 2 ( k g ) .
Vì khi pha dao động là π/2 thì vân tốc của vật là − 20 3 cm/s suy ra:
V max = 20 3 ( c m / s )
⇒ A = V max ω = 20 3 π ( c m )
x 1 = 3 π ( c m ) = 3 2 A
⇒ W d 1 = 1 4 W = 1 4 . 1 2 . k . A 2
= 1 8 .20. 20 3 π .100 2 = 0 , 03 ( J )

Câu 64: Một vật dao động điều hoà trên trục x’0x với chu kỳ T = 0,5s, Gốc toạ độ O là vị trí cân bằng của vật. Lúc t = 0 vât đi qua vị trí có li độ x = 3 cm, và vận tốc bằng 0. Phương trình dao động của vật:
A. x = 5cos(4π.t)(cm) B. x = 5cos(4π .t +π)(cm)
C. x = 3cos(4π.t +π)(cm) D. x = 3cos(4π.t)(cm)

+ Biên độ dao động: A = 40/2 = 10 cm.
+ Áp dụng: \(A^2 = x^2 +\frac{v^2}{\omega^2} \Rightarrow \omega = \sqrt{\frac{v^2}{A^2-x^2}} \Rightarrow \omega = 2\pi \Rightarrow T =1 \ s\)

Dùng công thức độc lập
\(x^2+\frac{v^2}{\omega^2}=A^2\)
Ta có:
\(\begin{cases}3^2+\frac{\left(8\pi\right)^2}{\omega^2}=A^2\\4^2+\frac{\left(6\pi\right)^2}{\omega^2}=A^2\end{cases}\)\(\Leftrightarrow\begin{cases}A=5\\\omega=2\sqrt{10}\end{cases}\)
\(\Rightarrow T=\frac{2\pi}{\omega}=1\left(s\right)\\ 2s=2T\Leftrightarrow S=8A=40cm\)

Đáp án C.
Xét
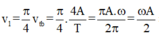
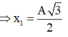
Vùng tốc độ ≥ v 1 nằm trong - x 1 ; x 1
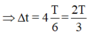 kết hợp với bài ta có T=0,5(s)
kết hợp với bài ta có T=0,5(s)
Phân tích 1 6 = T 3 quãng đường lớn nhất vật đi được trong T 3 khi vật đi qua lân cận vị trí cân bằng
Công thức
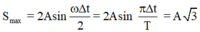 ,
,
đối chiếu với giả thiết ta có A=2(cm)
Vận tốc cực đại của vật trong quá trình chuyển động
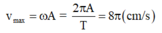

\(t=\dfrac{1}{3}s=\dfrac{T}{6}\)
Trong thời gian này, biểu diễn bằng véc tơ quay thì véc tơ đã quay được 1 góc là: \(\alpha=\dfrac{360}{6}=60^0\)
Quãng đường lớn nhất khi tốc độ trung bình trong thời gian này là lớn nhất, do vậy vật dao động quanh vị trí cân bằng với góc quay tương ứng là \(60^0\).
Biểu diễn trên véc tơ quay như sau:
5 -5 O M N 30 30
Quãng đường lớn nhất là đoạn MN
\(MN=2.5.\sin 30^0=5(cm)\)

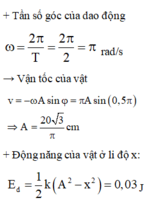
Nửa chu kỳ vật đi được quãng đường S=2A=10\(\Rightarrow A=5\left(cm\right)\)
Dùng công thức độc lập:
\(A^2=x^2+\frac{v^2}{\omega^2}\Leftrightarrow5^2=3^2+\frac{\left(16\pi\right)^2}{\omega^2}\Rightarrow\omega=4\pi\\ \Rightarrow T=\frac{1}{2}\left(s\right)\)
S=10 =>A=5
A2=x2 +v2/ω2 =>ω2=v2/(A2-x2) =>ω=4π
=>T=2π/ω=2π/4π=1/2=0,5s