Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo bài ra ta có:
W=Wđ+Wt =1/2.m.v2 +1/2.k.x2= 5.1/2.k.x2
Khi wt =4wđ thì cơ năng ở đó là:
w=wđ+wt = 5/4.wt = 5/4.1/2.kx'2
Theo định luật bảo toàn cơ năng cho hai vị trí ta có:
5/4.1/2.kx'^2 = 5.1/2.k.x^2 -> x' = ...

Độ dãn tối đa \(\Delta l_o=\frac{mg}{k}\)
Vận tốc lớn nhất \(v_{max}=\omega A=\sqrt{\frac{k}{m}}\frac{mg}{k}=g\sqrt{\frac{m}{k}}\)

Đáp án A
+ Do bỏ qua mọi lực cản nên cơ năng của con lắc lò xo bảo toàn vậy nó bằng cơ năng ở vị trí bài cho tức là ở vị trí có:
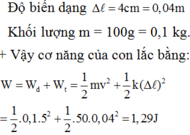

Đáp án C
Khi một vật chỉ chịu tác dụng của lực đàn hồi gây bởi sự biến dạng của một lò xo đàn hồi thì cơ năng của vật là một đại lượng bảo toàn:
![]()

Bài 1.
a)Thế năng: \(W_t=mgz=0,5\cdot10\cdot15=75J\)
b)Động năng vật:
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot0,5\cdot10^2=25J\)
Bài 2.
\(\Delta l=10cm=0,1m\)
Thế năng đàn hồi:
\(W_t=\dfrac{1}{2}k\cdot\left(\Delta l\right)^2=\dfrac{1}{2}\cdot100\cdot0,1^2=0,5J\)

a) Độ lớn của lực đàn hồi:
![]()
b) Thế năng đàn hồi:
![]()
c) Công thực hiện của lò xo:
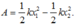
thay số:
![]()
Công A<0 vì lực đàn hồi ngược với chiều biến dạng, công của lực đàn hồi là công cản.

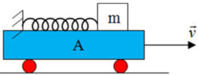
+ Chọn hệ quy chiếu gắn vào xe A
+ Ta có, các lực tác dụng vào m: F d h ; F q t ; N ; P
Vật m nằm cân bằng trên mặt phẳng của xe A nên:
F d h = F q t ↔ K . Δ l = m a → Δ l = m a K = 0 , 4.4 50 = 0 , 032 m = 3 , 2 c m
Đáp án: A

a. Ta có lực đàn hồi
F = k . | Δ l | ⇒ k = F | Δ l | ⇒ k = 2 0 , 01 ⇒ k = 200 N / m W t d h = 1 2 k . ( Δ l ) 2 = 1 2 .100.0 , 01 2 = 5.10 − 3 ( J )
b. Theo độ biến thiên thế năng
A = 1 2 k . ( Δ l 1 ) 2 − 1 2 k . ( Δ l 2 ) 2 = 1 2 .100 ( 0 , 02 2 − 0 , 035 2 ) = - 0 , 04125 ( J )
 10
10
a)Cơ năng vật: \(W=\dfrac{1}{2}k\left(\Delta l\right)^2=\dfrac{1}{2}\cdot50\cdot0,05^2=0,0625J\)
b)Vận tốc khi lò xo bị biến dạng:
\(\dfrac{1}{2}mv^2=W\Rightarrow v=\sqrt{\dfrac{2W}{m}}=\sqrt{\dfrac{2\cdot0,0625}{0,8}}=0,4\)m/s
c)Khi \(W_đ=W_t\Rightarrow W'=2W_t=2mgz\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow0,0625=2mgz\Rightarrow z=\dfrac{0,0625}{2\cdot0,8\cdot10}\approx4\cdot10^{-3}m=4mm\)
a) Cơ năng:
\(W_t=\dfrac{1}{2}mv^2+\dfrac{1}{2}k\left(\Delta l\right)^2=\dfrac{1}{2}\times0.8\times0^2+\dfrac{1}{2}\times50\times0.05^2=0.0625\left(J\right)\)
Do bỏ qua sức cản môi trường nên cơ năng bảo toàn
\(W_1=W=0.0625\left(J\right)\)
b) Vận tốc khi lò xo ko bị biến dạng:
\(0.0625=\dfrac{1}{2}\times0.8\times v^2+\dfrac{1}{2}\times50\times0^2\)
\(\Leftrightarrow v\approx0.4\)\((m/s)\)
c) \(W_đ=W_t\Leftrightarrow\left\{{}\begin{matrix}W_đ-W_t=0\\W_đ+W_t=0.0625\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}W_đ=0.03125\\W_t=0.03125\end{matrix}\right.\)
Khi \(W_đ=W_t\)
\(\Leftrightarrow W_t=\dfrac{1}{2}\times50\times\left(\Delta l\right)^2\)
\(\Leftrightarrow0.03125=\dfrac{1}{2}\times50\times\left(\Delta l\right)^2\)
\(\Leftrightarrow\Delta l\approx0.035\left(m\right)\)