Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

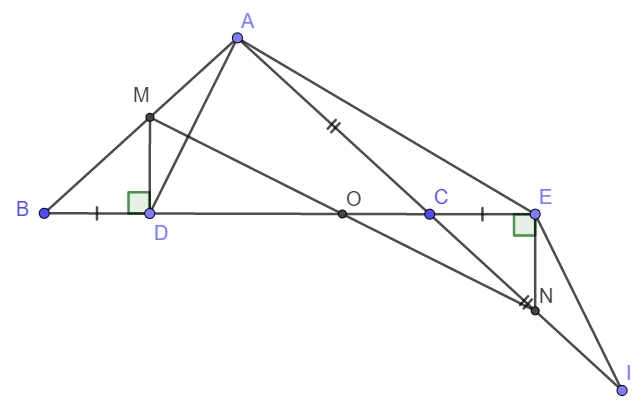
1)
+) Ta thấy \(\widehat{ECI}=\widehat{ACB}\) (Hai góc đối đỉnh)
Mà \(\widehat{ACB}=\widehat{ABC}\) (Tam giác ABC cân tại A)
nên \(\widehat{ECI}=\widehat{DBA}\)
Xét tam giác ABD và tam giác ICE có:
BD = CE (gt)
\(\widehat{DBA}=\widehat{ECI}\left(cmt\right)\)
CI = BA ( Cùng bằng AC)
\(\Rightarrow\Delta ABD=\Delta ICE\left(c-g-c\right)\)
+) Xét tam giác AEI, theo bất đẳng thức trong tam giác, ta có:
AI > AE + EI
Lại có do \(\Delta ABD=\Delta ICE\Rightarrow AD=IE\)
Vậy nên ta có AI > AE + AD \(\Rightarrow2AC>AD+AE\Rightarrow AB+AC>AD+AE\)
2) Do \(\Delta ABD=\Delta ICE\Rightarrow\widehat{MBD}=\widehat{NCE}\)
Vậy thì ta thấy ngay \(\Delta BDM=\Delta CEN\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow BM=CN\)
3) Ta thấy AB + AC = AM + MB + AC = AM + CN + AC = AM + AN
Ta cần chứng minh BC < MN.
Do BD = EC nên AC = DE
Xét tam giác vuông MDO ta có DO < MO (Quan hệ đường vuông góc, đường xiên)
Ta cũng có OE < ON
Vậy nên DE < MN hay BC < MN
Từ đó: AB + AC + BC < AM + AN + MN
Hay \(P_{AMN}>P_{ABC}\)

1. a) \(2009-\left|x-2009\right|=x\)
\(\Rightarrow\left|x-2009\right|=2009-x\)
\(\Rightarrow\left|x-2009\right|=-\left(x-2009\right)\)
\(\Rightarrow x-2009\le0\)
\(\Rightarrow x\le2009\)
Vậy \(x\le2009.\)
b) Ta có: \(\left[{}\begin{matrix}\left(2x-1\right)^{2008}\ge0\forall x\\\left(y-\dfrac{2}{5}\right)^{2008}\ge0\forall y\\\left|x+y-z\right|\ge0\forall x,y,z\end{matrix}\right.\) \(\Rightarrow\left(2x-1\right)^{2008}+\left(y-\dfrac{2}{5}\right)^{2008}+\left|x+y-z\right|\ge0\forall x,y,z\)
Dấu \("="\) xảy ra khi \(\left[{}\begin{matrix}\left(2x-1\right)^{2008}=0\\\left(y-\dfrac{2}{5}\right)^{2008}=0\\\left|x+y-z\right|=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{2}{5}\\z=\dfrac{9}{10}\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{2}{5}\\z=\dfrac{9}{10}\end{matrix}\right.\).
Bạn kia làm câu 1 rồi thì mình làm câu 2 nhé!
2. Ta có:\(\dfrac{3a-2b}{5}=\dfrac{2c-5a}{3}=\dfrac{5b-3c}{2}\)
\(\Rightarrow\dfrac{15a-10b}{25}=\dfrac{6c-15a}{9}=\dfrac{5b-3c}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{15a-10b}{25}=\dfrac{6c-15a}{9}=\dfrac{15a-10b+6c-15a}{25+9}\)=\(\dfrac{-10b+6c}{34}=\dfrac{-5b+3c}{17}\)
\(\Rightarrow\dfrac{-5b+3c}{17}=\dfrac{5b-3c}{2}\Rightarrow5b-3c=0\)
=> 5b=3c =>\(\left\{{}\begin{matrix}b=\dfrac{3}{5}c\\a=\dfrac{2}{5}c\end{matrix}\right.\)
=>\(\dfrac{3}{5}c+\dfrac{2}{5}c+c=-50\)
=> \(c\left(\dfrac{3}{5}+\dfrac{2}{5}+1\right)=-50\)
=> 2c = -50
=> c= -25
=>\(\left\{{}\begin{matrix}b=-25.\dfrac{3}{5}=-15\\a=-25.\dfrac{2}{5}=-10\end{matrix}\right.\)
Vậy a= -10; b= -15; c= -25

Ta luôn có :|x-2009|\(\ge\)0(1)
Mà :2009-|x-2009|=x nên 2009\(\ge\)x(2)
Vì (1)và(2) nên ta có x \(\in\){0;1;2;3;4;5;...;2009}

a )
ta có : \(\widehat{C_1}=\widehat{C_2}\) ( 2 góc đối đỉnh )
mà \(\widehat{C_1}=\widehat{B}\) ( tam gíac ABC cân tại A )
Do do : \(\widehat{C_2}=\widehat{B}\)
xét \(\Delta ABDva\Delta ICE,co:\)
AB = AC = IC ( gt )
BD=CE ( gt )
\(\widehat{C_2}=\widehat{B}\) (cmt )
Do do : \(\Delta ABD=\Delta ICE\left(c-g-c\right)\)

mình chỉ làm cho bạn câu a) thôi nhé. còn lại bạn cố gắng suy nghĩ nha vì mình ko có nhiều time
a) Ta xét hai tam giác ABD và ICE
Ta có: - AB= IC( cùng cạnh AC)
- góc ABD= ICE ( cùng bằng góc ACD:g. ABD= g.ACD vì 2 góc đấy tam giác cân ABC, g.ICE = g.ACD vì 2 góc đối đỉnh)
- BD=CE( giả thiết)
Vậy tam giác ABD= tam giác ICE ( c.g.c)
NHỚ TICK NHA!![]()
Chúc bạn mày mò ra bài
1: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
Do đó: ΔABD=ΔACE
2: Xét ΔDBM vuông tại D và ΔECN vuông tại E có
BD=CE
góc DBM=góc ECN
Do đó: ΔDBM=ΔECN
Suy ra: BM=CN

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Thị Ngọc Ánh - Toán lớp 7 - Học toán với OnlineMath

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau
Câu 3:
Giải:
Ta có: \(\frac{3a-2b}{5}=\frac{2c-5a}{3}=\frac{5b-3c}{2}\)
\(\Rightarrow\frac{15a-10b}{25}=\frac{6c-15a}{9}=\frac{10b-6c}{4}=\frac{15a-10b+6c-15a+10-6c}{25+9+4}=\frac{0}{25+9+4}=0\)
\(\Rightarrow\left\{\begin{matrix}\frac{15a-10b}{25}=0\\\frac{6c-15a}{9}=0\\\frac{10b-6c}{4}=0\end{matrix}\right.\Rightarrow\left\{\begin{matrix}15a-10b=0\\6c-15a=0\\10b-6c=0\end{matrix}\right.\Rightarrow\left\{\begin{matrix}15a=10b\\6c=15a\\10b=6c\end{matrix}\right.\)
\(\Rightarrow15a=10b=6c\)
\(\Rightarrow\frac{15a}{30}=\frac{10b}{30}=\frac{6c}{30}\)
\(\Rightarrow\frac{a}{2}=\frac{b}{3}=\frac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}=\frac{a+b+c}{2+3+5}=\frac{-50}{10}=-5\)
\(\Rightarrow\left\{\begin{matrix}a=-10\\b=-15\\c=-25\end{matrix}\right.\)
Vậy \(a=-10;b=-15;c=-25\)
3.Từ \(\dfrac{3a-2b}{5}=\dfrac{2c-5a}{3}=\dfrac{5b-3c}{2}\)
\(\Rightarrow\dfrac{15a-10b}{25}=\dfrac{6c-15a}{9}=\dfrac{10b-6c}{4}\)
Áp dụng tc dãy tỉ số bằng nhau ta có :
\(\dfrac{15a-10b}{25}=\dfrac{6c-15a}{9}=\dfrac{10b-6c}{4}=\dfrac{15a-10b+6c-15a+10b-6c}{25+4+9}=\dfrac{0}{25+4+9}=0\)
Áp dụng tc dãy tỉ số bằng nhau ta có :
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{10}=\dfrac{a+b+c}{4+6+10}=\dfrac{-50}{20}=\dfrac{-5}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}a=-10\\b=-15\\c=-25\end{matrix}\right.\)