Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hok nhanh phết, chưa j đã đến phần toạ độ vecto r
1/ \(\overrightarrow{MB}=\left(x_B-x_M;y_B-y_M\right)=\left(2-x_M;3-y_M\right)\)
\(\Rightarrow2\overrightarrow{MB}=\left(4-2x_M;6-2y_M\right)\)
\(\overrightarrow{3MC}=\left(3x_C-3x_M;3y_C-3y_M\right)=\left(-3-3x_M;6-3y_M\right)\)
\(\Rightarrow2\overrightarrow{MB}+3\overrightarrow{MC}=\left(4-2x_M-3-3x_M;6-2y_M+6-3y_M\right)=0\)
\(\Leftrightarrow\left(1-5x_M;12-5y_M\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-5x_M=0\\12-5y_M=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_M=\frac{1}{5}\\y_M=\frac{12}{5}\end{matrix}\right.\Rightarrow M\left(\frac{1}{5};\frac{12}{5}\right)\)
2/ \(\overrightarrow{m}=2\left(1;2\right)+3\left(3;4\right)=\left(2+9;4+12\right)=\left(11;16\right)\)
3/ \(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)=\left(-5-3;4+2\right)=\left(-8;6\right)\)
\(\overrightarrow{AC}=\left(x_C-x_A;y_C-y_A\right)=\left(\frac{1}{3}-3;0+2\right)=\left(-\frac{8}{3};2\right)\)
\(\Rightarrow x=\frac{\overrightarrow{AB}}{\overrightarrow{AC}}=\frac{\left(-8;6\right)}{\left(-\frac{8}{3};2\right)}=3\)
Câu 4 tương tự
Câu 5 vt lại đề bài nhé bn, nghe nó vô lý sao á, m,n ở đâu ra vậy, cả A,B,C nx

a) \(\overrightarrow{u}=3\overrightarrow{a}+2\overrightarrow{b}-4\overrightarrow{c}=3\left(2;1\right)+2\left(3;-4\right)-4\left(-7;2\right)\)
\(=\left(6;3\right)+\left(6;-8\right)-\left(-28;8\right)\)
\(=\left(6+6+28;3-8-8\right)=\left(40;-13\right)\).
b) \(\overrightarrow{x}+\overrightarrow{a}=\overrightarrow{b}-\overrightarrow{c}\Leftrightarrow\overrightarrow{x}=\overrightarrow{b}-\overrightarrow{c}-\overrightarrow{a}\)
\(\Leftrightarrow\overrightarrow{x}=\left(3;-4\right)-\left(-7;2\right)-\left(2;1\right)\)
\(\Leftrightarrow\overrightarrow{x}=\left(3+7-2;-4-2-1\right)\)
\(\Leftrightarrow\overrightarrow{x}=\left(8;-7\right)\).
c) Có \(\overrightarrow{c}\left(-7;2\right)=k\overrightarrow{a}+h\overrightarrow{b}=k\left(2;1\right)+h\left(3;-4\right)\)
\(=\left(2k+3h;k-4h\right)\).
Từ đó suy ra: \(\left\{{}\begin{matrix}2k+3h=-7\\k-4h=2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}k=-2\\h=-1\end{matrix}\right.\).

\(\left(a+2b\right)^2=28\Leftrightarrow a^2+4b^2+4ab=28\)
\(\Rightarrow ab=\frac{28-4^2-4.3^2}{4}=-6\)
\(\Rightarrow cos\left(a;b\right)=-\frac{6}{4.3}=-\frac{1}{2}\Rightarrow\left(a;b\right)=120^0\)

\(A^2=\left|3a+5b\right|^2=9a^2+25b^2+30ab=9.1+25.1+30.3=124\)
\(\Rightarrow A=2\sqrt{31}\)

\(u.v=0\Leftrightarrow\left(2a+3b\right)\left(-15a+14b\right)=0\)
\(\Leftrightarrow-30a^2+42b^2-17ab=0\)
\(\Leftrightarrow ab=\frac{-30.4^2+42.3^2}{17}=-6\)
\(\Rightarrow cos\left(a;b\right)=\frac{ab}{\left|a\right|\left|b\right|}=-\frac{6}{12}=-\frac{1}{2}\Rightarrow\left(a;b\right)=120^0\)

b) \(\left|\overrightarrow{a}+\overrightarrow{b}\right|=\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|\) khi vectơ a và vectơ b cùng hướng

a) cos(;
) =
= 0
=> (;
) = 900
b) cos(;
) =
=
=> (;
) = 450
c) cos(;
) =
=
=> (;
) = 1500
Đăng những câu khác đi em mỏi tay rồi
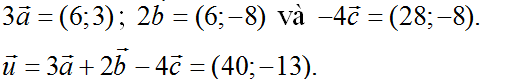

Bài 1:
\(\overrightarrow{OM}=\left(-2;1\right)\) ; \(\overrightarrow{ON}=\left(3;-1\right)\)
\(\Rightarrow cos\widehat{MON}=\frac{-2.3-1.1}{\sqrt{4+1}.\sqrt{9+1}}=-\frac{7\sqrt{2}}{10}\)
Gọi \(A\left(a;0\right)\Rightarrow\overrightarrow{AM}=\left(-2-a;1\right)\); \(\overrightarrow{AN}=\left(3-a;-1\right)\)
\(\widehat{MAN}=90^0\Rightarrow\overrightarrow{AM}.\overrightarrow{AN}=0\)
\(\Rightarrow\left(-2-a\right)\left(3-a\right)-1.1=0\)
\(\Leftrightarrow a^2-a-7=0\Rightarrow a=\frac{1\pm\sqrt{29}}{2}\)
Bài 2:
a/ \(\overrightarrow{a}.\overrightarrow{b}=0\Leftrightarrow3.4-2.5m=0\Rightarrow10m=12\Rightarrow m=\frac{6}{5}\)
b/ \(\overrightarrow{a}.\overrightarrow{b}=0\Leftrightarrow9.1-16m.4m=0\Leftrightarrow64m^2=9\)
\(\Rightarrow m^2=\frac{9}{64}\Rightarrow m=\pm\frac{3}{16}\)
Bài 3:
\(\overrightarrow{OA}=\left(2;0\right)\) ; \(\overrightarrow{AB}=\left(0;2\right)\) ; \(\overrightarrow{CB}=\left(2;0\right)\); \(\overrightarrow{OC}=\left(0;2\right)\)
\(\Rightarrow\overrightarrow{OA}=\overrightarrow{CB}\Rightarrow OABC\) là hbh
\(\overrightarrow{OA}.\overrightarrow{AB}=2.0+0.2=0\Rightarrow OA\perp AB\)
\(\Rightarrow OABC\) là hcn (hbh có 1 góc vuông)
\(\left\{{}\begin{matrix}OA=\sqrt{2^2+0^2}=2\\AB=\sqrt{0^2+2^2}=2\end{matrix}\right.\) \(\Rightarrow OA=AB\)
\(\Rightarrow OABC\) là hình vuông (hcn có 2 cạnh kề bằng nhau)
Bài 4:
Phương trình đường thẳng \(\Delta\): \(x-y-2=0\)
Áp dụng công thức khoảng cách:
\(d\left(A;\Delta\right)=\frac{\left|1-1-2\right|}{\sqrt{1^2+\left(-1\right)^2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\)