KK
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
YN
1
29 tháng 2 2020
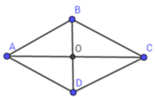
A B C D O AC = 8 BD = 6
Gọi \(O\) là giao điểm của \(AC\)và \(BD\).
Theo đề ta có: \(\hept{\begin{cases}AC=8cm\\BD=6cm\end{cases}}\)
Theo tính chất của hình thoi ta có: \(\hept{\begin{cases}AO=OC=4cm\\BO=OD=3cm\end{cases}}\)
Áp dụng định lí Pitago trong \(\Delta AOB\) có:
\(AB^2=AO^2+OB^2\)
\(\Rightarrow AB=\sqrt{AO^2+OB^2}=\sqrt{4^2+6^2}\)
\(\Rightarrow AB=5cm\)
\(\Rightarrow S_{ABCD}=4AB=4.5=20cm\)
Vậy ...............
CM
5 tháng 11 2019
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 20 2 − 16 2 = 12
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.12.16 = 384 (cm2)
Đáp án cần chọn là: A
CM
9 tháng 5 2017
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 10 2 − 6 2 = 8
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.8.6 = 96 (cm2)
Đáp án cần chọn là: B
YN
3
CC
29 tháng 2 2020
Gọi O là giao điểm của 2 đường chéo của hình thoi
\(\Rightarrow\)O là trung điểm của AC và BD
\(\Rightarrow OA=\frac{1}{2}AC=\frac{1}{2}.8=4\left(cm\right)\)và \(OB=\frac{1}{2}BD=\frac{1}{2}.6=3\left(cm\right)\)
Tứ giác ABCD là hình thoi \(\Rightarrow AC\perp BD\)\(\Rightarrow OA\perp OB\)\(\Rightarrow\Delta OAB\)vuông tại O
Áp dụng định lý Pytago ta có: \(OA^2+OB^2=AB^2\)
\(\Rightarrow AB^2=4^2+3^2=16+9=25\)\(\Rightarrow AB=5\left(cm\right)\)
Vì ABCD là hình thoi \(\Rightarrow AB=BC=CD=CA\)
\(\Rightarrow P_{ABCD}=4.AB=4.5=20\left(cm\right)\)
29 tháng 2 2020
\(S_{ABCD}=\frac{1}{2}AC\cdot BD=\frac{1}{2}\cdot8\cdot16=64\left(cm^2\right)\)