Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

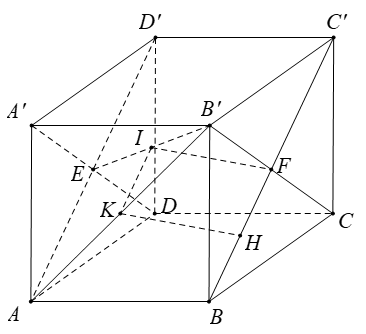
1. Do \(EG||AC\Rightarrow\widehat{\left(\overrightarrow{AF};\overrightarrow{EG}\right)}=\widehat{\left(\overrightarrow{AF};\overrightarrow{AC}\right)}=\widehat{FAC}\)
Mà \(AF=AC=CF=AB\sqrt{2}\Rightarrow\Delta ACF\) đều
\(\Rightarrow\widehat{FAC}=60^0\)
2.
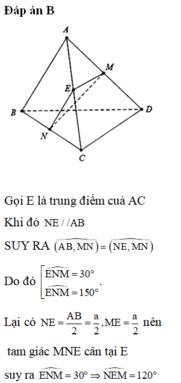
Do I;J lần lượt là trung điểm SC, BC \(\Rightarrow IJ\) là đường trung bình tam giác SBC
\(\Rightarrow IJ||SB\)
Lại có \(CD||BA\Rightarrow\widehat{\left(IJ;CD\right)}=\widehat{SB;BA}=\widehat{SBA}=60^0\) (do các cạnh của chóp bằng nhau nên tam giác SAB đều)

\(A'C'=\sqrt{a^2+a^2}=a\sqrt{2}\)
=>\(A'C=\sqrt{\left(a\sqrt{2}\right)^2+\left(a\sqrt{3}\right)^2}=a\sqrt{5}\)


b) Ta có ACC' là tam giác vuông có cạnh \(AC=a\sqrt{2},CC'=a\)
Vậy \(AC'^2=AC^2+CC^2\Rightarrow AC'^2=2a^2+a^2=3a^2\)
Vậy \(AC'=a\sqrt{3}\)