Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tần số góc ω = 2π/T, trong đó T là chu kỳ dao động (6s).
Pha ban đầu φ = 0, vì tại thời điểm t1 vật chuyển động theo chiều dương.
Thời gian di chuyển từ thời điểm t1 đến t2: Δt = t2 - t1 = 0,9s.
Vận tốc của vật tại thời điểm t2 là:
v = 10cm * (2π/6 rad/s) * cos((2π/6 rad/s) * (0,9s)).

Đáp án D
E chuyển động quanh hạt nhân với quỹ đạo
là đường tròn lực cu lông đóng vai trò làm lực hướng tâm


Tốc độ lớn nhất hay nhỏ nhất ứng với quãng đường lớn nhất và nhỏ nhất.
Chu kì dao động của P: \(T=2\pi/\omega=4s\)
\(t=1s=T/4\), trong thời gian này chất điểm M quay một góc là: \(360/4=90^0\)
+ P có quãng đường lớn nhất ứng với chuyển động quanh VTCB, mỗi bên 1 góc \(45^0\), quãng đường: \(S=2.4.\cos 45^0=4\sqrt 2(cm)\)
\(\Rightarrow v = 4\sqrt 2(cm/s)\)
+ P có quãng đường nhỏ nhất ứng với chuyển động quanh biên, mỗi bên 1 góc \(45^0\), quãng đường:
\(S=2.(4-4.\cos45^0)=8-4\sqrt 2(cm)\)
\(\Rightarrow v = 8-4\sqrt 2 cm\)

Chọn C
+ Phương trình dao động: x = Acos(ωt + φ).
+ Tìm các đại lượng:
* A: Có giá trị bằng một nửa quỹ đạo dài => A = 5 cm = 0,05m.
* ω: ω = 2πf = 4π rad/s.
* Tìm φ:
t = 0: v = -ωAsinφ < 0 => sinφ > 0 (1).
t = 2 (s): a = -ω2Acos(4πt + φ) = -ω2Acos(8π + φ) = -8cosφ = 4√3 m/s.
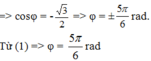
+ Thay vào các phương trình trên => x = 5cos(4πt +5π/6)(cm).