Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x,y,z,t lần lượt là số cây trồng được của lớp 7A1,7A2,7A3,7A4
(x,y,z,t ∈ N * )
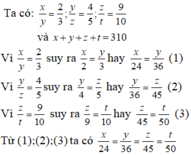
Với x + y + z + t = 172 , áp dụng tính chất dãy tỉ số bằng nhau ta có
x 24 = y 36 = z 45 = t 50 = x + y + z + t 24 + 36 + 45 + 50 = 310 155 = 2
Suy ra z 45 = 2 nên t = 45.2 = 90 (tm)
Số cây của lớp 7A4 trồng được là 90 cây
Đáp án cần chọn là B

Lời giải:
Gọi số cây trồng lớp 7A1, 7A2, 7A3 lần lượt là $a,b,c$. Theo bài ra:
$\frac{a}{3}=\frac{b}{7}=\frac{c}{5}$
$b-c=48$
Áp dụng TCDTSBN:
$\frac{a}{3}=\frac{b}{7}=\frac{c}{5}=\frac{b-c}{7-5}=\frac{48}{2}=24$
$\Rightarrow a=3.24=72; b=7.24=168; c=5.24=120$
gọi số cây của ba lớp 7A1 ; 7A ; 7A3 trồng được là x;y ; z ( cây ). x; y; z thuộc N sao
vì số cây của ba lớp tỉ lệ với 3 , 7 ,5 nên ta có x/3=y/7=z/5
vì số cây của lớp 7A3 trồng ít hơn số cây cuả lớp 7A2 là 48 cây nên ta có y -z = 48
áp dụng tính chất của dãy tỉ số bằng nhau ta có :
x/3=y/7=z/5 =y-z/7-5 =24
x/3 = 24 suy ra x=24*3 = 72
y/7 =24 suy ra y= 24*7 = 168
z/5=24 suy ra z= 24*5=120
vậy x= 72
y=168
z = 120

Gọi x,y,z lần lượt là số cây trồng của lớp 7A1 ,7A2 và 7A3. ta có
Số cây ba lớp trồng được lần lượt tỉ lệ với các số 3; 5;2⇒\(\frac{x}{3}\)=\(\frac{y}{5}\)=\(\frac{z}{2}\)
7A1 trồng được ít hơn lớp 7A2 là 50 cây⇒y−x=50
Áp dụng tính chất của dãy tỉ số bằng nhau ta có ⇒\(\frac{x}{3}\)=\(\frac{y}{5}\)=\(\frac{z}{2}\)=\(\frac{y-x}{5-3}\)=\(\frac{50}{2}\)=25
tứ đây suy ra x=75, y=125, z=50 cây
Gọi số cây 3 lớp 7A1 ; 7A2 và 7A3 lần lượt là a ; b ; c ( câu ) ( a , b , c ∈ N* )
Theo bài ra , ta có :
b - a = 50
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{2}=\frac{b-a}{5-3}=\frac{50}{2}=25\)
\(\Rightarrow\hept{\begin{cases}a=25.3=75\\b=25.5=125\\c=25.2=50\end{cases}}\)

Gọi x,y,z lần lượt là số cây trồng của lớp 7A1 ,7A2 và 7A3. ta có
Số cây ba lớp trồng được lần lượt tỉ lệ với các số 3; 5;2\(\Rightarrow\frac{x}{3}=\frac{y}{5}=\frac{z}{2}\)
7A1 trồng được ít hơn lớp 7A2 là 50 cây\(\Rightarrow y-x=50\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có \(\Rightarrow\frac{x}{3}=\frac{y}{5}=\frac{z}{2}=\frac{y-x}{5-3}=\frac{50}{2}=25\)
tứ đây suy ra x=75, y=125, z=50 cây

Gọi số cây 3 lớp lần lượt là: a,b,c
Ta có:
a/4 = b/3 = c/5 và a + b + c = 180
Áp dụng tính chất dãy tỉ số bằng nhau, có:
\(\frac{a}{4}=\frac{b}{3}=\frac{c}{5}=\frac{a+b+c}{4+3+5}=\frac{180}{12}=15\)
Suy ra: \(\frac{a}{4}=15\Rightarrow a=15\cdot4=60\)
\(\frac{b}{3}=15\Rightarrow b=15\cdot3=45\)
\(\frac{c}{5}=15\Rightarrow c=15\cdot5=75\)
Vậy ..........
Giải
Ta có sơ đồ
Lớp 7a1 : |------------|------------|------------|------------|
Lớp 7a2 : |------------|------------|------------|
Lớp 7a3 : |------------|------------|------------|------------|------------|
Tổng số phần bằng nhau là :
4 + 3 + 5 = 12 ( phần )
Số cây lớp 7a1 trồng là :
180 : 12 x 4 = 60 ( cây )
Số cây lớp 7a2 trồng là :
180 : 12 x 3 = 45 ( cây )
Số cây lớp 7a3 trồng là :
180 : 12 x 5 = 75 ( cây )
Đáp số : Lớp 7a1 : 60 cây
Lớp 7a2 : 45 cây
Lớp 7a3 : 75 cây

Gọi số cây trồng được của 3 lớp 7A ; 7B ; 7C lần lượt là x,y,z (x,y,z \(\inℕ^∗\))
Theo bài ra ta có :
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}\)và \(2x-y=8\)
=> \(\frac{2x}{4}=\frac{y}{3}=\frac{z}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau có:
\(\frac{2x}{4}=\frac{y}{3}=\frac{z}{5}=\frac{2x-y}{2.2-3}=\frac{8}{1}=8\)
=> x = 8 . 2 =16
y = 8 . 3 = 24
z = 8 . 5 = 40
Vậy............................................
Học tốt