Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{3x^3+10x^2-9x-4}{\left(x-1\right)\left(x^2+2x-8\right)}=4\)
<=> \(\frac{\left(x+4\right)\left(x-1\right)\left(3x+1\right)}{\left(x-1\right)\left(x-2\right)\left(x+4\right)}=4\)
<=> \(\frac{3x+1}{x-2}=4\)
<=> 3x + 1 = 4(x - 2)
<=> 3x + 1 = 4x - 8
<=> 4x - 3x = 8 + 1
<=> x = 9
Vậy tập nghiệm của pt là \(S=\left\{9\right\}\)

c: \(=\dfrac{1}{3x-2}-\dfrac{4}{3x+2}+\dfrac{3x-6}{\left(3x-2\right)\left(3x+2\right)}\)
\(=\dfrac{3x+2-12x+8+3x-6}{\left(3x-2\right)\left(3x+2\right)}\)
\(=\dfrac{-6x+4}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{-2}{3x+2}\)
d: \(=\dfrac{x^2-4-x^2+10}{x+2}=\dfrac{6}{x+2}\)
e: \(=\dfrac{1}{2\left(x-y\right)}-\dfrac{1}{2\left(x+y\right)}-\dfrac{y}{\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{x+y-x+y-2y}{2\left(x-y\right)\left(x+y\right)}=\dfrac{0}{2\left(x-y\right)\left(x+y\right)}=0\)

\(A=\left(x+1\right)^3-\left(x+3\right)^2\left(x+1\right)+4x^2+8\)
\(A=x^3+3x^2+3x+1-\left(x^2+6x+9\right)\left(x+1\right)+4x^2+8\)
\(A=x^3+3x^2+3x+1-\left(x^3+6x^2+9x+x^2+6x+9\right)+4x^2+8\)
\(A=x^3+3x^2+3x+1-x^3-6x^2-9x-x^2-6x-9+4x^2+8\)
\(A=\left(x^3-x^3\right)+\left(3x^2-6x^2-x^2+4x^2\right)+\left(3x-9x-6x\right)+\left(1-9+8\right)\)
\(A=-12x\)
\(B=\left(x-2\right)\left(x^2+2x+4\right)-\left(x+1\right)^3+3\left(x-1\right)\left(x+1\right)\)
\(B=x^3+2x^2+4x-2x^2-4x-8-\left(x^3+3x^2+3x+1\right)+3\left(x^2-1\right)\)
\(B=x^3+2x^2+4x-2x^2-4x-8-x^3-3x^2-3x-1+3x^2-3\)
\(B=\left(x^3-x^3\right)+\left(2x^2-2x^2-3x^2+3x^2\right)+\left(4x-4x-3x\right)+\left(-8-3-1\right)\)
\(B=-3x-12\)
Câu C tương tự.
Chúc bạn học tốt!!!
A = \(\left(x+1\right)^3-\left(x+3\right)^2.\left(x+1\right)+4x^2+8\)
A = \(\left(x+1\right)\left(x+1-x-3\right)\left(x+1+x+3\right)+4x^2+8\)
A = \(\left(x+1\right).\left(-2\right).\left(2x+4\right)+4x^2+8\)
A = \(\left(-2\right)\left(2x^2+4x+2x+4\right)+4x^2+8\)
A = \(\left(-2\right)\left(2x^2+6x+4\right)+4x^2+8\)
A = \(-4x^2-12x-8+4x^2+8=-12x\)
b) B = \(\left(x-2\right)\left(x^2+2x+4\right)-\left(x+1\right)^3+3\left(x-1\right)\left(x+1\right)\)
B = \(x^3-8-\left(x+1\right)\left(x^2+2x+1+3x-3\right)\)
B = \(x^3-8-\left(x+1\right)\left(x^2+5x-2\right)\)
B = \(x^3-8-x^3-5x^2+2x-x^2-5x+2\)
B = \(-6x^2-3x-6\)

Bài 1:
a) \(9x^2-6x+2\)
\(\Leftrightarrow9x^2-6x+1+1\)
\(\Leftrightarrow\left(3x-1\right)^2+1\)
Vì \(\left(3x-1\right)^2\ge0\forall x,1>0\)
\(\Rightarrow9x^2-6x+2\) luôn dương với mọi x.
b) \(x^2+x+1\)
\(\Leftrightarrow x^2+x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Vì \(\left(x+\dfrac{1}{2}\right)^2\ge0\forall x,\dfrac{3}{4}>0\)
\(\Rightarrow x^2+x+1\) luôn dương với mọi x.
Bài 2 :
a) \(A=x^2-3x+5\)
\(\Leftrightarrow A=x^2-3x+2+3\)
\(\Leftrightarrow A=\left(x-2\right)\left(x-1\right)+3\)
Vì \(\left(x-2\right)\left(x-1\right)\ge0\forall x\) => \(A\ge3\)
Vậy GTNN A đạt được = 3 khi và chỉ khi x = 2 hoặc x = 1.
b) \(B=\left(2x-1\right)^2+\left(x+2\right)^2\)
\(\Leftrightarrow B=4x^2-4x+1+x^2+4x+4\)
\(\Leftrightarrow B=5x^2+5\)
\(\Leftrightarrow B=5\cdot\left(x^2+1\right)\)
Vì \(x^2+1\ge1\forall x\)
=> GTNN của B đạt được = 5 khi và chỉ khi x = 0.
Bài 3 :
a) \(A=-x^2+2x+4\)
Làm tương tự ta có \(A_{MAX}=5\) khi và chỉ khi x = 1.
b) \(B=-x^2+4x\)
Làm tương tự ta có \(B_{MAX}=4\) khi và chỉ khi x = 2.

a) \(\left(3x-1\right)\left(2x+7\right)-\left(x+1\right)\left(6x-5\right)=16\) (1)
\(\Leftrightarrow6x^2+21x-2x-7-\left(6x^2-5x+6x-5\right)=16\)
\(\Leftrightarrow6x^2+21x-2x-7-\left(6x^2+x-5\right)=16\)
\(\Leftrightarrow6x^2+21x-2x-7-6x^2-x+5=16\)
\(\Leftrightarrow18x-2=16\)
\(\Leftrightarrow18x=16+2\)
\(\Leftrightarrow18x=18\)
\(\Leftrightarrow x=1\)
Vậy tập nghiệm phương trình (1) là \(S=\left\{1\right\}\)
b) \(\left(10x+9\right)\cdot x-\left(5x-1\right)\left(2x+3\right)=8\) (2)
\(\Leftrightarrow10x^2+9x-\left(10x^2+15x-2x-3\right)=8\)
\(\Leftrightarrow10x^2+9x-\left(10x^2+13x-3\right)=8\)
\(\Leftrightarrow10x^2+9x-10x^2-13x+3=8\)
\(\Leftrightarrow-4x+3=8\)
\(\Leftrightarrow-4x=8-3\)
\(\Leftrightarrow-4x=5\)
\(\Leftrightarrow x=-\dfrac{5}{4}\)
Vậy tập nghiệm phương trình (2) là \(S=\left\{-\dfrac{5}{4}\right\}\)
c) \(\left(3x-5\right)\left(7-5x\right)+\left(5x+2\right)\left(3x-2\right)-2=0\) (3)
\(\Leftrightarrow21x-15x^2-35+25x+15x^2-10x+6x-4-2=0\)
\(\Leftrightarrow42x-41=0\)
\(\Leftrightarrow42x=41\)
\(\Leftrightarrow x=\dfrac{41}{42}\)
Vậy tập nghiệm phương trình (3) là \(S=\left\{\dfrac{41}{42}\right\}\)
d) \(x\left(x+1\right)\left(x+6\right)-x^3=5x\) (4)
\(\Leftrightarrow\left(x^2+x\right)\left(x+6\right)-x^3=5x\)
\(\Leftrightarrow x^3+6x^2+x^2+6x-x^3=5x\)
\(\Leftrightarrow7x^2+6x=5x\)
\(\Leftrightarrow7x^2+6x-5x=0\)
\(\Leftrightarrow7x^2+x=0\)
\(\Leftrightarrow x\left(7x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\7x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{7}\end{matrix}\right.\)
Vậy tập nghiệm phương trình (4) là \(S=\left\{-\dfrac{1}{7};0\right\}\)

1. \(A=x^2-2x+5\)
\(=\left(x^2-2x+1\right)+4\)
\(=\left(x-1\right)^2+4\)
Vì \(\left(x-1\right)^2\ge0\forall x\) nên \(\left(x-1\right)^2+4\ge4\forall x\)
Dấu "=" \(\Leftrightarrow\) x - 1 = 0 \(\Leftrightarrow\) x = 1
Vậy ...
2. \(B=-2x^2-4x+1\)
\(=-2\left(x^2+2x-\dfrac{1}{2}\right)\)
\(=-\left(x^2+2x+1-\dfrac{3}{2}\right)\)
\(=-\left(x+1\right)^2+\dfrac{3}{2}\le\dfrac{3}{2}\forall x\)
Dấu "=" \(\Leftrightarrow\) x + 1 = 0 \(\Leftrightarrow\) x = -1
Vậy ...
3. \(C=\dfrac{3}{-x^2+2x-4}\)
\(=-\dfrac{3}{x^2-2x+4}\)
\(=-\dfrac{3}{\left(x^2-2x+1\right)+3}\)
\(=-\dfrac{3}{\left(x-1\right)^2+3}\)
Vì \(\left(x-1\right)^2\ge0\) nên \(\left(x-1\right)^2+3\ge3\)
\(\Rightarrow-\dfrac{3}{\left(x-1\right)^2+3}\ge-\dfrac{3}{3}=-1\)
Dấu "=" \(\Leftrightarrow\) x - 1 = 0 \(\Leftrightarrow\) x = 1
Vậy ...
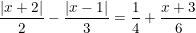


1) \(2x-\left|6x-7\right|=-x+8\)
\(\Rightarrow\orbr{\begin{cases}2x-\left(6x-7\right)=-x+8\\2x-\left(-6x+7\right)=-x+8\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}-3x=1\\9x=15\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{3}\\x=\frac{5}{3}\end{cases}}\)
Thử lại đều không thỏa mãn.
Vậy phương trình vô nghiệm.
2) \(\frac{\left|x+2\right|}{2}-\frac{\left|x-1\right|}{3}=\frac{1}{4}+\frac{x+3}{6}\)(2)
Với \(x\ge1\): (2) tương đương với:
\(\frac{x+2}{2}-\frac{x-1}{3}=\frac{1}{4}+\frac{x+3}{6}\)
\(\Leftrightarrow0x=-\frac{7}{12}\)(phương trình vô nghiệm)
Với \(-2\le x< 1\): (2) tương đương với:
\(\frac{x+2}{2}-\frac{1-x}{3}=\frac{1}{4}+\frac{x+3}{6}\)
\(\Leftrightarrow\frac{2}{3}x=\frac{1}{12}\Leftrightarrow x=\frac{1}{8}\)(thỏa mãn)
Với \(x< -2\): (2) tương đương với:
\(\frac{-x-2}{2}-\frac{1-x}{3}=\frac{1}{4}+\frac{x+3}{6}\)
\(\Leftrightarrow\frac{-1}{3}x=\frac{25}{12}\Leftrightarrow x=-\frac{25}{4}\)(thỏa mãn)
3) \(\left|x^2-2x\right|=x\)
\(\Rightarrow\orbr{\begin{cases}x^2-2x=x\\x^2-2x=-x\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2-3x=0\\x^2-x=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=0,x=3\\x=0,x=1\end{cases}}\)
Thử lại đều thỏa mãn.
4) \(\left|x^2-4x+5\right|=x^2-1\)
\(\Leftrightarrow x^2-4x+5=x^2-1\)(vì \(x^2-4x+5=\left(x-2\right)^2+1>0\))
\(\Leftrightarrow-4x=-6\)
\(\Leftrightarrow x=\frac{3}{2}\)