K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LH
0
LA
9 tháng 1 2024
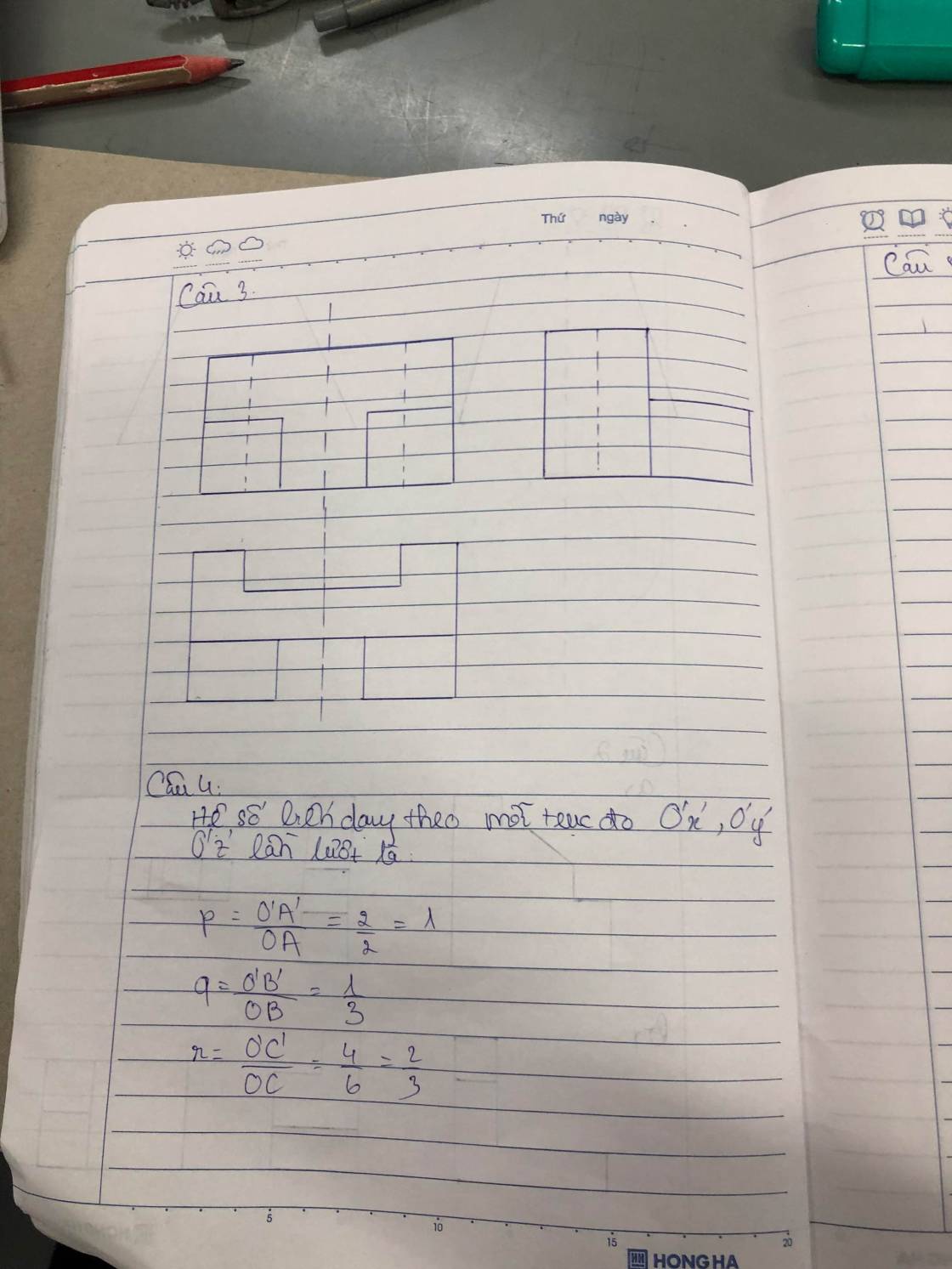
Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a)
Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng lớn (dần tới \( + \infty \)).
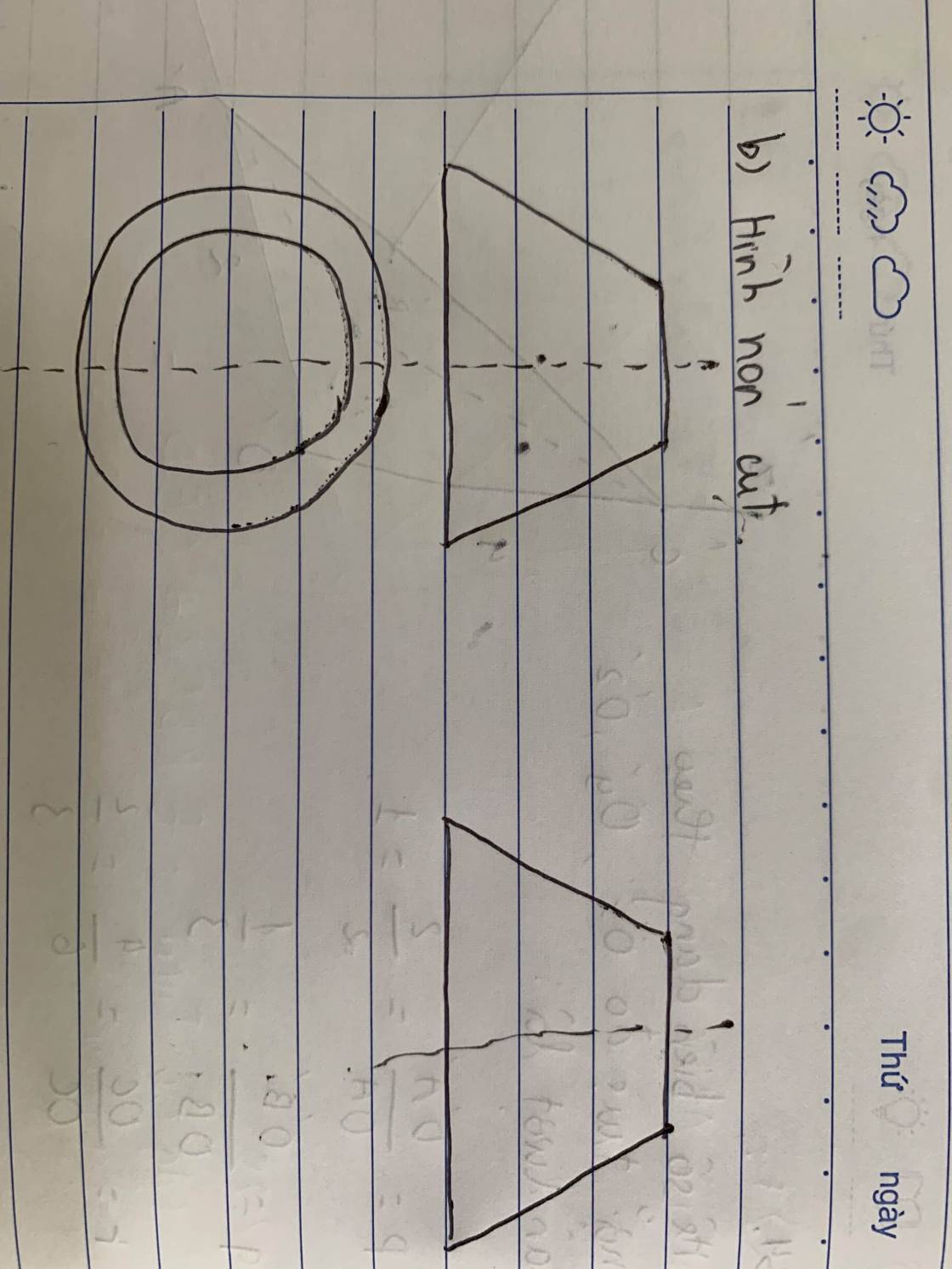
b)
Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng bé (dần tới \( - \infty \)).
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
1.
\(u_{n+1}=4u_n+3.4^n\)
\(\Leftrightarrow u_{n+1}-\dfrac{3}{4}\left(n+1\right).4^{n+1}=4\left[u_n-\dfrac{3}{4}n.4^n\right]\)
Đặt \(u_n-\dfrac{3}{4}n.4^n=v_n\Rightarrow\left\{{}\begin{matrix}v_1=2-\dfrac{3}{4}.4=-1\\v_{n+1}=4v_n\end{matrix}\right.\)
\(\Rightarrow v_n=-1.4^{n-1}\)
\(\Rightarrow u_n=\dfrac{3}{4}n.4^n-4^{n-1}=\left(3n-1\right)4^{n-1}\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
2.
\(a_n=\dfrac{a_{n-1}}{2n.a_{n-1}+1}\Rightarrow\dfrac{1}{a_n}=2n+\dfrac{1}{a_{n-1}}\)
\(\Leftrightarrow\dfrac{1}{a_n}-n^2-n=\dfrac{1}{a_{n-1}}-\left(n-1\right)^2-\left(n-1\right)\)
Đặt \(\dfrac{1}{a_n}-n^2-n=b_n\Rightarrow\left\{{}\begin{matrix}b_1=2-1-1=0\\b_n=b_{n-1}=...=b_1=0\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{a_n}=n^2+n\Rightarrow a_n=\dfrac{1}{n^2+n}\)
TD
52
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 10 2019
ĐKXĐ: \(-2\le x\le3\)
Đặt \(\sqrt{x+2}+2\sqrt{3-x}=a\Rightarrow4\sqrt{6+x-x^2}-3x=a^2-14\)
Mặt khác \(a^2=\left(\sqrt{x+2}+2\sqrt{3-x}\right)^2\le5\left(x+2+3-x\right)=25\)
\(\Rightarrow a\le5\)
Và \(\sqrt{x+2}+\sqrt{3-x}+\sqrt{3-x}\ge\sqrt{5}+\sqrt{3-x}\ge\sqrt{5}\) \(\Rightarrow a\ge\sqrt{5}\)
\(\Rightarrow\sqrt{5}\le a\le5\)
Phương trình trở thành:
\(a^2-14=ma\Leftrightarrow\frac{a^2-14}{a}=m\) với \(a\in\left[\sqrt{5};5\right]\)
\(f\left(a\right)=\frac{a^2-14}{a}\Rightarrow f'\left(a\right)=\frac{2a^2-a^2+14}{a^2}=\frac{a^2+14}{a^2}>0\)
\(\Rightarrow f\left(a\right)\) đồng biến \(\Rightarrow f\left(\sqrt{5}\right)\le f\left(a\right)\le5\)
\(\Rightarrow-\frac{9\sqrt{5}}{5}\le f\left(a\right)\le\frac{11}{5}\Rightarrow-\frac{9\sqrt{5}}{5}\le m\le\frac{11}{5}\)
a.
Do chóp S.ABCD đều \(\Rightarrow SO\perp\left(ABCD\right)\)
\(\Rightarrow\) O là hình chiếu vuông góc của S lên (ABCD)
\(\Rightarrow\Delta OAB\) là hình chiếu vuông góc của \(\Delta SAB\) lên (ABCD)
b.
Gọi E là trung điểm CD \(\Rightarrow OE\) là đường trung bình tam giác BCD
\(\Rightarrow OE||BC\Rightarrow OE\perp CD\)
\(\Rightarrow CD\perp\left(SOE\right)\)
Trong mp (SOE), từ O kẻ \(OK\perp SE\)
\(OK\in\left(SOE\right)\Rightarrow CD\perp OK\)
\(\Rightarrow OK\perp\left(SCD\right)\)
Trong mp (ACK), qua A kẻ đường thẳng song song OK cắt CK kéo dài tại H
\(\Rightarrow AH\perp\left(SCD\right)\Rightarrow SH\) là hình chiếu vuông góc của SA lên (SCD)
\(\Rightarrow\widehat{ASH}\) là góc giữa SA và (SCD) hay \(\widehat{ASH}=\varphi\)
\(OE=\dfrac{1}{2}BC=\dfrac{a}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông SOE:
\(OK=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{5}}{5}\)
O là trung điểm AC và \(OK||SH\Rightarrow OK\) là đường trung bình tam giác CAH
\(\Rightarrow AH=2OK=\dfrac{2a\sqrt{5}}{5}\)
\(OA=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\Rightarrow SA=\sqrt{SO^2+OA^2}=\dfrac{a\sqrt{6}}{2}\)
\(\Rightarrow sin\varphi=\dfrac{AH}{SA}=\dfrac{2\sqrt{30}}{15}\)