K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NL
1
AD
20 tháng 8 2023
Kẻ Az//Bx//Dy
=> BAD = BAz + DAz = (180o - ABx) + (180o - ADy) = 30o + 60o = 90o
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 8
Olm chào em, vì em tặng coin mà tài khoản của em chỉ có chưa tới 50 coin thì không tặng được, em nhé.
Còn bạn tăng xu nên vẫn tặng được vì tài khoản của bạn trên 50 xu
Nếu em muốn chuyển tiền cho bạn thì em phải đổi từ coin sang xu rồi mới có đủ tiền để tặng bạn.
Lưu ý coin có thể cho, tặng, đổi quà.. đổi sang xu.
Còn xu thì không thể chuyển sang coin. chỉ đổi quà và tặng bạn thôi em ơi.
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
QT
1
18 tháng 9 2023
Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:
\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
KV
25 tháng 1 2024
\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)
AH
Akai Haruma
Giáo viên
31 tháng 1 2024
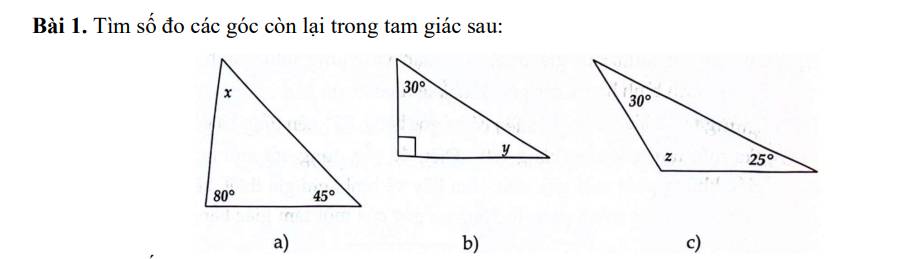
Lời giải:
Áp dụng tính chất tổng 3 góc trong một tam giác bằng $180^0$
a.
$x=180^0-80^0-45^0=55^0$
b.
$y=180^0-30^0-90^0=60^0$
c.
$z=180^0-30^0-25^0=125^0$
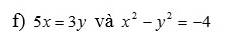
Bài 4 :
Ta có :
\(\widehat{ABC}=100^o\)
\(\widehat{BCD}=40+60=100^o\)
\(\Rightarrow\widehat{ABC}=\widehat{BCA}=100^o\) ở vị trí sole trong
\(\Rightarrow AB//CD\left(1\right)\)
Ta lại có :
\(\widehat{MCD}=60^o\)
Kẻ thêm từ MN qua trái 1 đường thẳng tạo thành 1 góc \(\widehat{CMx}\)
\(\Rightarrow\widehat{CMx}=180-120=60^o\)
\(\widehat{MCD}=\widehat{CMx}=60^o\) ở vị trí sole trong
\(\Rightarrow MN//CD\left(2\right)\)
\(\left(1\right).\left(2\right)\Rightarrow\Rightarrow AB//MN\)
1. Bài 4.
Ta có: AB//CD ( góc so le trong)
Mặt khác: góc MCD + góc CMN = 180o nên 2 góc trên là 2 góc trong cùng phía bù nhau
==>CD//MN do AB//CD ==> AB//MN (đpcm)
2. Bài 5
Từ C kẻ đoạn thẳng CF // với AB và DE
Ta có góc BCF = góc ABC = 40o (so le trong) (1)
góc FCE = góc CED = 30o (so le trong) (2)
Từ 1 và 2 suy ra góc BCE = góc BCF + góc FCE = 40o +30o =70o